甲与乙两人掷硬币，甲用一枚硬币掷3次，记正面朝上的次数为
；乙用这枚硬币掷2次，记正面朝上的次数为
。
（1）分别求与的期望；
（2）规定：若
，则甲获胜；若
，则乙获胜，分别求出甲和乙获胜的概率.
已知直线
经过点
，且倾斜角为
，圆M以
为圆心，过极点．
（I）求与M的极坐标方程；
（II）判断与M的位置关系．
已知
，命题
，命题
．
（I）若命题
为真命题，求实数
的取值范围；
（II）若命题
为假命题，求实数的取值范围．
（本小题满分12分）
若函数
满足下列两个性质：
①在其定义域上是单调增函数或单调减函数；
②在的定义域内存在某个区间使得在
上的值域是
．则我们称为“内含函数”．
（1）判断函数
是否为“内含函数”？若是，求出a、b，若不是，说明理由；
（2）若函数
是“内含函数”，求实数t的取值范围．
（本小题满分12分）
铁路运输托运行李，从甲地到乙地，规定每张客票托运费计算方法是：行李质量不超过50 kg时，按0．25元/kg计算；超过50 kg而不超过100 kg时，其超过部分按0．35元/kg计算；超过100 kg时，其超过部分按0．45元/kg计算．
（1）计算出托运费用；
（2）若行李质量为56 kg，托运费用为多少？
（本小题满分12分）
若f（x）是定义在（0，＋∞）上的增函数，且对一切x，y＞0，满足f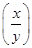
＝f（x）－f（y）．
（1）求f（1）的值；
（2）若f（6）＝1，解不等式f（x＋3）－f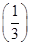
＜2．