计算物体在下列时间段内的加速度。(取初速度方向为正方向)
(1)以40m/s做匀速直线运动的汽车,遇紧急情况刹车,经8s停下。
(2)一小球从斜面上由静止下滑,3s末滑至底端,速度为6m/s。
一根长为L的丝线吊着一质量为m,电荷量为q的小球静止在水平向右的匀强电场中,如图所示,丝线与竖直方向成370角,现突然将该电场方向变为向下且大小不变,不考虑因电场的改变而带来的其他影响(重力加速度为g)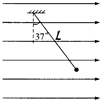 (sin370=0.6,cos370="0.8)" 求:
(sin370=0.6,cos370="0.8)" 求:匀强电场的电场强度的大小
小球经过最低点时丝线的拉力。
把q1= 4×10-9C的试探电荷放在电场中的A点,具有6×10-8J的电势能,求A点的电势.若把q2= -2×10-10C的试探电荷放在电场中的A点,电荷所具有的电势能是多少?
15.(10分) 如图所示,R1=2Ω,R2=R3=4Ω.当S接A时,外电路消耗的电功率为4W;当S接B时,电压表示数为4.5v。
求: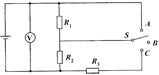
电源的电动势和内电阻
当S接c时,R1消耗的电功率
如图所示,质量M="8" kg的小车放在水平光滑的平面上,在小车左端加一水平推力F="8" N,当小车向右运动的速度达到1.5 m/s时,在小车前端轻轻地放上一个大小不计,质量为m="2" kg的小物块,物块与小车间的动摩擦因数为0.2,小车足够长.求:
小物块刚放上小车时,小物块及小车的加速度各为多大?
经多长时间两者达到相同的速度?
从小物块放上小车开始,经过t="1.5" s小物块通过的位移大小为多少?(取g="l0" m/s2).
一水平传送带以2.0m/s的速度顺时针传动,水平部分长为2.0m。,其右端与一倾角为θ=37°的光滑斜面平滑相连,斜面长为0.4m,一个可视为质点的物块无初速度地放在传送带最左端,已知物块与传送带间动摩擦因数μ=0.2,试问:物块到达传送带右端的速度。
物块能否到达斜面顶端?若能则说明理由,若不能则求出物块上升的最大高度.
(sin37°=0.6, g取l0 m/s2)
2011年7月23日20时34分在温州方向双屿路段下岙路,发生了严重的动车追尾事故,此次事故造成六节车厢脱轨。现假设有一列快车正以60m/s的速度在平直的铁轨上行驶时,发现前面1000m处有一货车正以18m/s的速度匀速同向行驶,快车立即合上制动器,以2 m/s2的加速度做匀减速直线运动,试判断两车是否发生撞车事故.