用数学归纳法证明(n+1)(n+2)(n+3)…(n+n)=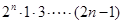 (n∈N*)时,从n=k到n=k+1,左端需要增加的代数式为( )
(n∈N*)时,从n=k到n=k+1,左端需要增加的代数式为( )
| A.2k+1 | B.2(2k+1) | C.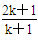 |
D.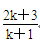 |
若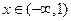 ,则函数
,则函数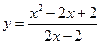 有()
有()
A.最小值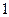 |
B.最大值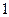 |
C.最大值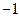 |
D.最小值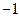 |
设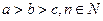 ,且
,且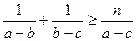 恒成立,则
恒成立,则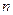 的最大值是()
的最大值是()
A.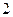 |
B.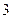 |
C.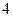 |
D.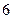 |
若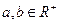 ,且
,且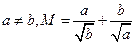 ,
, 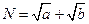 ,则
,则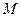 与
与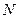 的大小关系是
的大小关系是
A.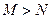 |
B.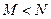 |
C.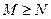 |
D.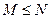 |
已知一几何体的三视图如下,正视图和侧视图都是矩形,俯视图为正方形,在该几何体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是(写出所有正确结论的编号).
①矩形;
②不是矩形的平行四边形;
③有三个面为直角三角形,有一个面为等腰三角形的四面体;
④每个面都是等腰三角形的四面体;
⑤每个面都是直角三角形的四面体.
设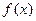 是定义在正整数集上的函数,且
是定义在正整数集上的函数,且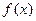 满足:“当
满足:“当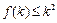 成立时,总可推出
成立时,总可推出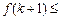
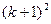 成立”.那么,下列命题总成立的是
成立”.那么,下列命题总成立的是
A.若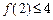 成立,则当 成立,则当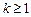 时,均有 时,均有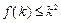 成立 成立 |
B.若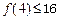 成立,则当 成立,则当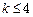 时,均有 时,均有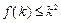 成立 成立 |
C.若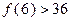 成立,则当 成立,则当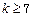 时,均有 时,均有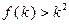 成立 成立 |
D.若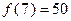 成立,则当 成立,则当 时,均有 时,均有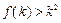 成立 成立 |