为普及高中生安全逃生知识与安全防护能力,某学校高一年级举办了高中生安全知识与安全逃生能力竞赛. 该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛.先将所有参赛选手参加笔试的成绩(得分均为整数,满分为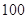 分)进行统计,制成如下频率分布表.
分)进行统计,制成如下频率分布表.
| 分数(分数段) |
频数(人数) |
频率 |
| [60,70) |
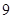 |
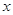 |
| [70,80) |
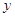 |
 |
| [80,90) |
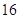 |
 |
| [90,100) |
 |
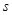 |
| 合 计 |
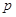 |
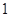 |
(Ⅰ)求出上表中的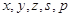 的值;
的值;
(Ⅱ)按规定,预赛成绩不低于 分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一·二班有甲、乙两名同学取得决赛资格.
分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一·二班有甲、乙两名同学取得决赛资格.
①求决赛出场的顺序中,甲不在第一位、乙不在最后一位的概率;
②记高一·二班在决赛中进入前三名的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
(本小题 满分12分)已知 是定义在
是定义在 上的偶函数,且
上的偶函数,且 时,
时, .
.
(1)求 ,
, ;
;
(2)求函数 的表达式;
的表达式;
(3)若 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)已知命题p: 命题q:1-m≤x≤1+m,m>0,
命题q:1-m≤x≤1+m,m>0,
若¬p是¬q的必要不充分条件,求实数m的取值范围.
(本小题满分10分)已知函数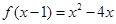 ,求函数
,求函数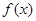 ,
,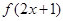 的解析式.
的解析式.
(本大题13分)已知函数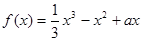 (
(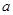 为常数)
为常数)
(1)若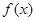 在区间
在区间 上单调递减,求
上单调递减,求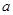 的取值范围;
的取值范围;
(2)若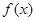 与直线
与直线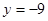 相切:
相切:
(ⅰ)求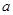 的值;
的值;
(ⅱ)设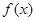 在
在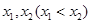 处取得极值,记点M (
处取得极值,记点M ( ,
,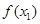 ),N(
),N(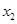 ,
,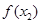 ),P(
),P(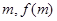 ),
),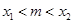 , 若对任意的m
, 若对任意的m 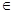 (
( , x
, x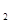 ),线段MP与曲线f(x)均有异于M,P的公共点,试确定
),线段MP与曲线f(x)均有异于M,P的公共点,试确定 的最小值,并证明你的结论.
的最小值,并证明你的结论.
(本大题9分)已知大于1的正数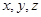 满足
满足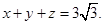
(1)求证: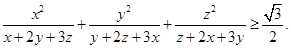
(2)求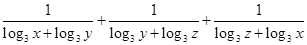 的最小值.
的最小值.