在一个盒子中，放有大小相同的红、白、黄三个小球，现从中任意摸出一球，若是红球记1分，白球记2分，黄球记3分．现从这个盒子中有放回地先后摸出两球，所得分数分别记为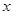
、
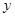，设
为坐标原点，点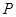
的坐标为
，记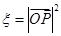
．
(1)求随机变量
=5的概率；
(2)求随机变量的分布列和数学期望．
(本小题满分12分)
△ABC中，A（– 4，2）．
（1）若∠
ACB的平分线CD所在直线方程为
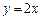，B（3，1），求点C的坐标；
（2）若两条中线所在直线分别为
，求直线
BC的方程．
(本小题满分13分)
(1)已知圆C经过P（4，– 2），Q（–1，3)两点，若圆心C在直线y = 2x上，求圆C的方程；
(2)已知圆M经过坐标原点O，圆心M在直线
上，与x轴的另一个交点为A，△MOA为等腰直角三角形，求圆M的方程．
(本小题满分13分)
已知实数
满足
．
(1)求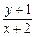
的取值范围；
(2)求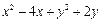
的取值范围．
(本小题满分13分)
(1)椭圆C与椭圆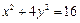
有相同焦点，且椭圆C上一点P到两焦点的距离之和等于
，求椭圆C的标准方程；
(2)椭圆的两个焦点F1、F2在x轴上，以| F1F2|为直径的圆与椭圆的一个交点为（3，4），求椭圆标准方程．
设数列
的前n项和为
，对任意的正整数n，都有
成立，记
（
），
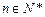（１）求数列
的通项公式；
（2）记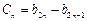
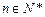（），设数列
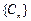的前n和为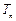
，求证：对任意正整数n，都有
．