铁路部门托运行李的收费方法如下:y是收费额(单位:元),x是行李重量(单位:㎏),当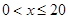 时,按0.35/㎏ 收费,当
时,按0.35/㎏ 收费,当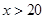 ㎏ 时,20㎏的部分按0.35元/㎏,超出20㎏的部分,则按0.65元/㎏收费.
㎏ 时,20㎏的部分按0.35元/㎏,超出20㎏的部分,则按0.65元/㎏收费.
⑴ 请根据上述收费方法求出Y关于X的函数式;
⑵画出流程图并写出程序。
计算:
(1)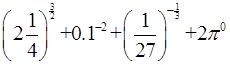 ;
;
(2)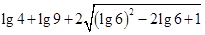
我国是水资源比较贫乏的国家之一,各地采用价格调控等手段以达到节约用水的目的。某市用水收费标准是:水费=基本费+超额费+定额损耗费,且有如下三条规定:
①若每月用水量不超过最低限量 立方米时,只付基本费9元和每户每月定额损耗费
立方米时,只付基本费9元和每户每月定额损耗费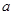 元;
元;
②若每月用水量超过 立方米时,除了付基本费9元和定额损耗费外,超过部分每立方米付
立方米时,除了付基本费9元和定额损耗费外,超过部分每立方米付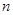 元的超额费;
元的超额费;
③每户每月定额损耗费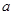 不超过5元。
不超过5元。
(1)求每户每月水费 (元)与月用水量
(元)与月用水量 (立方米)的函数关系式;
(立方米)的函数关系式;
(2)该市一家庭今年第一季度每月的用水量和支付的费用如下表所示:
| 月份 |
用水量(立方米) |
水费(元) |
| 一 |
4 |
17 |
| 二 |
5 |
23 |
| 三 |
2.5 |
11 |
试分析该家庭今年一、二、三各月份的用水量是否超过最低限量,并求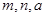 的值。
的值。
如图,四棱锥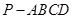 的底面是正方形,
的底面是正方形,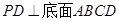 ,点E在棱PB上。
,点E在棱PB上。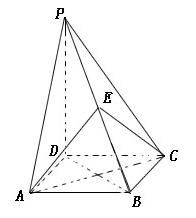
(Ⅰ)求证:平面 ;
;
(Ⅱ)当 且E为PB的中点时,求AE与平
且E为PB的中点时,求AE与平
面PDB所成的角的大小。
过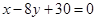 与
与 的交点的直线被圆
的交点的直线被圆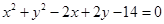 所截得的弦长为
所截得的弦长为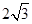 ,求此直线方程。
,求此直线方程。
已知关于 的方程
的方程 的两个根为
的两个根为
求: (1) 的值;
的值;
(2)实数 的值;
的值;
(3)方程的两个根及此时 的值
的值