我国是水资源比较贫乏的国家之一，各地采用价格调控等手段以达到节约用水的目的。某市用水收费标准是：水费=基本费+超额费+定额损耗费，且有如下三条规定：
①若每月用水量不超过最低限量
立方米时，只付基本费9元和每户每月定额损耗费
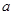元；
②若每月用水量超过立方米时，除了付基本费9元和定额损耗费外，超过部分每立方米付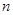
元的超额费；
③每户每月定额损耗费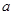不超过5元。
（1） 求每户每月水费
（元）与月用水量
（立方米）的函数关系式；
（2） 该市一家庭今年第一季度每月的用水量和支付的费用如下表所示：
| 月份 |
用水量（立方米） |
水费（元） |
| 一 |
4 |
17 |
| 二 |
5 |
23 |
| 三 |
2.5 |
11 |
试分析该家庭今年一、二、三各月份的用水量是否超过最低限量，并求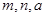
的值。
某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场，其总面积为3000平方米，其中场地四周（阴影部分）为通道，通道宽度均为2米，中间的三个矩形区域将铺设塑胶地面作为运动场地（其中两个小场地形状相同），塑胶运动场地占地面积为
平方米.
（1）分别写出用
表示
和用表示的函数关系式（写出函数定义域）；
（2）怎样设计能使S取得最大值，最大值为多少？
已知函数
，
（1）在如图给定的直角坐标系内画出
的图象；
（2）写出的单调递增区间.
已知函数
（1）求
的定义域；
（2）当
为何值时，函数值大于1.
(1)求不等式的解集：
．
(2)求函数的定义域：
．
已知函数
.
(Ⅰ)若曲线
在
和
处的切线互相平行，求
的值；
(Ⅱ)求
的单调区间；
(Ⅲ)设
，若对任意
，均存在
，使得
，求的取值范围.