解不等式(1)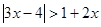 (2)解不等式
(2)解不等式
已知数列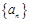 中,
中,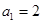 ,
, ,其前
,其前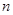 项和
项和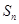
满足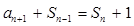
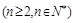 .
.
(Ⅰ)求证:数列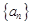 为等差数列,并求
为等差数列,并求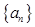 的通项公式;
的通项公式;
(Ⅱ)设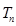 为数列
为数列 的前
的前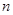 项和,求
项和,求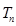
(Ⅲ)若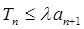 对一切
对一切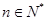 恒成立,求实数
恒成立,求实数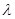 的最小值.
的最小值.
已知关于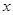 的不等式
的不等式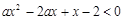
(1)当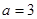 时,求此不等式解集;
时,求此不等式解集;
(2)当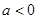 时,求此不等式解集。
时,求此不等式解集。
一种化学名为“尼美舒利”的儿童退热药,其药品安全性疑虑引起社会的关注,国家药监局调查了这种药的100个相关数据,绘制成如图所示的频率分布直方图,再对落在 两组内的数据按分层抽样方法抽取8个数据,然后再从这8个数据中抽取2个,(1)求最后所得这两个数据分别来自两组的概率?
两组内的数据按分层抽样方法抽取8个数据,然后再从这8个数据中抽取2个,(1)求最后所得这两个数据分别来自两组的概率?
(2)由所给的频率分布直方图估计样本数据的中位数?(精确到0.01)
在△ABC中,三内角A、B、C及其对边a、b、c,满足 ,
,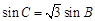
(Ⅰ)求角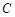 的大小(Ⅱ)若
的大小(Ⅱ)若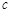 =6,求△ABC面积.
=6,求△ABC面积.
以下茎叶图记录了甲、乙两组五名同学的植树棵数,乙组记录中有一个数据模糊无法确认,在图中以X表示。
(Ⅰ)如果X=7,求乙组同学植树棵数的平均数和方差;
(Ⅱ)如果X=8,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为18或19的概率。