(本小题满分12分)设函数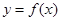 在
在 上的导函数为
上的导函数为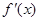 ,
,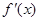 在
在 上的导函数为
上的导函数为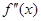 ,若在
,若在 上,
上,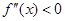 恒成立,则称函数
恒成立,则称函数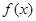 在
在 上为“凸函数”.已知
上为“凸函数”.已知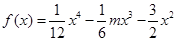 .
.
(1)若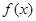 为区间
为区间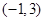 上的“凸函数”,试确定实数
上的“凸函数”,试确定实数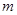 的值;
的值;
(2)若当实数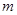 满足
满足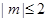 时,函数
时,函数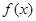 在
在 上总为“凸函数”,求
上总为“凸函数”,求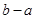 的最大值.
的最大值.
如图,有一段河流,河的一侧是以O为圆心,半径为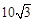 米的扇形区域OCD,河的另一侧是一段笔直的河岸l,岸边有一烟囱AB(不计B离河岸的距离),且OB的连线恰好与河岸l垂直,设OB与圆弧
米的扇形区域OCD,河的另一侧是一段笔直的河岸l,岸边有一烟囱AB(不计B离河岸的距离),且OB的连线恰好与河岸l垂直,设OB与圆弧 的交点为E.经测量,扇形区域和河岸处于同一水平面,在点C,点O和点E处测得烟囱AB的仰角分别为
的交点为E.经测量,扇形区域和河岸处于同一水平面,在点C,点O和点E处测得烟囱AB的仰角分别为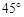 ,
,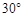 和
和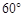 .
.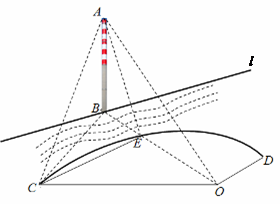
(1)求烟囱AB的高度;
(2)如果要在CE间修一条直路,求CE的长.
如图,四边形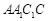 为矩形,四边形
为矩形,四边形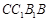 为菱形,且平面
为菱形,且平面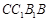 ⊥平面
⊥平面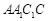 ,D,E分别为边
,D,E分别为边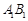 ,
,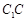 的中点.
的中点.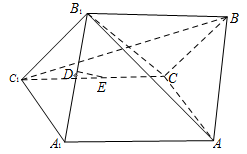
(1)求证: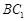 ⊥平面
⊥平面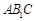 ;
;
(2)求证:DE∥平面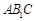 .
.
若存在 个不同的正整数
个不同的正整数 ,对任意
,对任意 ,都有
,都有 ,则称这
,则称这 个不同的正整数
个不同的正整数 为“
为“ 个好数”.
个好数”.
(1)请分别对 ,
, 构造一组“好数”;
构造一组“好数”;
(2)证明:对任意正整数 ,均存在“
,均存在“ 个好数”.
个好数”.
如图,在四棱锥P-ABCD中, 底面ABCD,底面ABCD是边长为2的菱形,
底面ABCD,底面ABCD是边长为2的菱形, ,
, ,M为PC的中点.
,M为PC的中点.
(1)求异面直线PB与MD所成的角的大小;
(2)求平面PCD与平面PAD所成的二面角的正弦值.
求函数 的最大值.
的最大值.