已知椭圆 和圆
和圆 :
: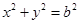 ,过椭圆上一点P引圆O的两条切线,切点分别为A,B.
,过椭圆上一点P引圆O的两条切线,切点分别为A,B. 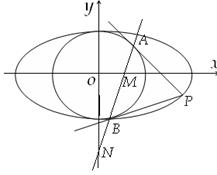
(1)(ⅰ)若圆O过椭圆的两个焦点,求椭圆的离心率e的值;
(ⅱ)若椭圆上存在点P,使得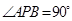 ,求椭圆离心率e的取值范围;
,求椭圆离心率e的取值范围;
(2)设直线AB与x轴、y轴分别交于点M,N,问当点P在椭圆上运动时, 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.
△ABC中,a、b、c分别是角A、B、C的对边,△ABC的周长为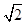 +2,且sinA+sinB=
+2,且sinA+sinB=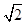 sinC.(1)求边c的长. (2)若△ABC的面积为
sinC.(1)求边c的长. (2)若△ABC的面积为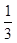 sinC,求角C的度数.
sinC,求角C的度数.
数列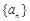 满足
满足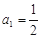 ,
,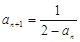
 .
.
(1)求证: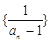 为等差数列,并求出
为等差数列,并求出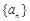 的通项公式;
的通项公式;
(2)设 ,数列
,数列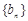 的前
的前 项和为
项和为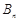 ,对任意
,对任意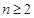 都有
都有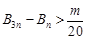 成立,求整数
成立,求整数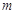 的最大值.
的最大值.
已知数列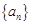 的前
的前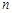 项和为
项和为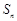 ,
,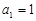 ,
, 是
是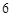 与
与 的等差中项(
的等差中项(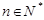 ).
).
(1)求数列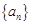 的通项公式;
的通项公式;
(2)是否存在正整数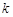 ,使不等式
,使不等式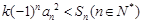 恒成立,若存在,求出
恒成立,若存在,求出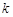
的最大值;若不存在,请说明理由.
在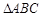 中,角
中,角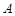 、
、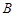 、
、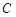 所对的边分别为
所对的边分别为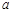 、
、 、
、 ,满足
,满足 .
.
(1)求角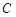 ;
;
(2)求 的取值范围.
的取值范围.
已知函数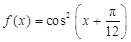 ,
,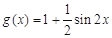 .
.
(1)设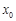 是函数
是函数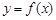 的一个零点,求
的一个零点,求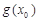 的值;
的值;
(2)求函数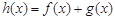 的单调递增区间.
的单调递增区间.