如图所示，足够长的斜面倾角θ＝370，一物体以v0=12m/s的初速度从斜面上A点处沿斜面向上运动；加速度大小为a=8m/s2，g取10m/s2．求:
(1)物体沿斜面上滑的最大距离x；
(2)物体与斜面间的动摩擦因数μ；
(3)物体从A点出发需经多少时间才能回到A处．
位于竖直平面内的矩形平面导线框abdc，ab长L1＝1.0 m，bd长L2＝0.5 m，线框的质量m＝0.2 kg，电阻R＝2 Ω.其下方有一匀强磁场区域，该区域的上、下边界PP′和QQ′均与ab平行．两边界间距离为H，H>L2，磁场的磁感应强度B＝1.0 T，方向与线框平面垂直。如图27所示，令线框的dc边从离磁场区域上边界PP′的距离为h＝0.7 m处自由下落．已知线框的dc边进入磁场以后，ab边到达边界PP′之前的某一时刻线框的速度已达到这一阶段的最大值．问从线框开始下落，到dc边刚刚到达磁场区域下边界QQ′的过程中，磁场作用于线框的安培力所做的总功为多少？(g取10 m/s2)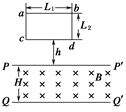
金属杆MN和PQ间距为l,MP间接有电阻R,磁场如图所示,磁感应强度为B.金属棒AB长为2l,由图示位置以A为轴,以角速度ω匀速转过90°(顺时针).求该过程中(其他电阻不计):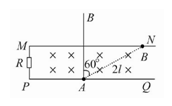
(1)R上的最大电功率.
(2)通过R的电量.
半径为a的圆形区域内有均匀磁场，磁感应强度为B="0.2" T，磁场方向垂直纸面向里，半径为b的金属圆环与磁场同心地放置，磁场与环面垂直，其中a="0.4" m，b =" 0.6" m，金属环上分别接有灯L1、L2，两灯的电阻均为R0 =" 2" Ω，一金属棒MN与金属环接触良好，棒与环的电阻均忽略不计.
(1)若棒以v0="5" m/s的速率在环上向右匀速滑动，求棒滑动到圆环直径OO′的瞬时(如图所示)，MN中的电动势和流过灯L1的电流.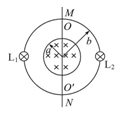
(2)撤去中间的金属棒MN将右面的半圆环OL2O′以OO′为轴向上翻转90°,若此时磁场随时间均匀变化，其变化率为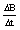
=
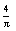T/s，求L2的功率.
右图电路中R1＝12 Ω，R2＝6 Ω，滑动变阻器R3上标有“20 Ω，2 A”字样，理想电压表的量程有0～3 V和0～15 V两挡，理想电流表的量程有0～0.6 A和0～3 A两挡．闭合开关S，将滑片P从最左端向右移动到某位置时，电压表、电流表示数分别为2.5 V和0.3 A；继续向右移动滑片P至另一位置，电压表指针指在满偏的1/3，电流表指针指在满偏的1/4，求：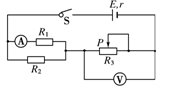
(1)此时电流表示数；
(2)电源的电动势．
一台小型电动机在3 V电压下工作，用此电动机提升所受重力为4 N的物体时，通过它的电流是0.2 A．在30 s内可使该物体被匀速提升3 m．若不计除电动机线圈生热之外的能量损失，求：
(1)电动机的输入功率；
(2)在提升重物的30 s内，电动机线圈所产生的热量；
(3)线圈的电阻．