设数列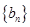 的前
的前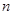 项和为
项和为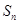 ,对任意的
,对任意的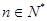 ,都有
,都有 ,且
,且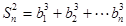 ;数列
;数列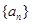 满足
满足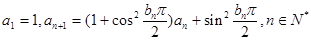 .
.
(Ⅰ)求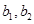 的值及数列
的值及数列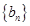 的通项公式;
的通项公式;
(Ⅱ)求证: 对一切
对一切 成立.
成立.
已知圆C:x2+y2-2x+4y-4=0,问是否存在斜率是1的直线l,使l被圆C截得的弦AB,以AB为直径的圆经过原点,若存在,写出直线l的方程;若不存在,说明理由.
一束光线l自A(-3,3)发出,射到x轴上,被x轴反射到⊙C:x2+y2-4x-4y+7=0上.(1)求反射线通过圆心C时,光线l的方程;(2)求在x轴上,反射点M的范围.
如图,四棱锥P—ABCD的底面ABCD为正方形,PD⊥底面ABCD,PD=AD.求证:(1)平面PAC⊥平面PBD;(2)求PC与平面PBD所成的角;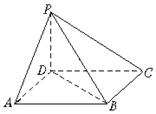
已知函数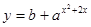 (
(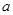 、b是常数且
、b是常数且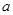 >0,
>0,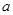 ≠1)在区间[-
≠1)在区间[-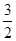 ,0]上有ymax=3,ymin=
,0]上有ymax=3,ymin=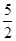 ,试求
,试求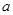 和b的值.[
和b的值.[
.求经过点A(-5,2)且在x轴上的截距等于在y轴上的截距的2倍的直线方程;