已知圆C:x2+y2-2x+4y-4=0,问是否存在斜率是1的直线l,使l被圆C截得的弦AB,以AB为直径的圆经过原点,若存在,写出直线l的方程;若不存在,说明理由.
如图,该曲线表示一人骑自行车离家的距离与时间的关系.骑车者9时离开家,15时回家.根据这个曲线图,请你回答下列问题: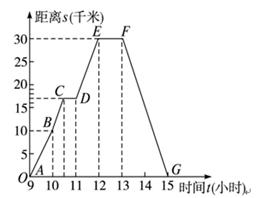
(1)最初到达离家最远的地方是什么时间?离家多远?
(2)何时开始第一次休息?休息多长时间?
(3)第一次休息时,离家多远?
(4)11:00到12:00他骑了多少千米?
(5)他在9:00~10:00和10:00~10:30的平均速度分别是多少?
(6)他在哪段时间里停止前进并休息用午餐?
求下列函数的定义域:
(1)y=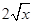 -
- ;
;
(2)y=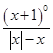
求下列函数的定义域:
(1)f(x)=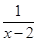 ;
;
(2)f(x)=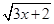 ;
;
(3)f(x)=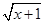 +
+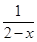 .
.
已知函数 在
在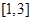 上有最大值
上有最大值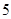 和最小值
和最小值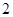 ,求
,求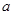 、
、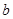 的值。
的值。
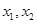 是关于
是关于 的一元二次方程
的一元二次方程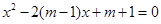 的两个实根,又
的两个实根,又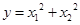 ,求
,求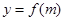 的解析式及此函数的定义域。
的解析式及此函数的定义域。