我市某林场计划购买甲、乙两种树苗共800株,甲种树苗每株24元,乙种树苗每株30元.相关资料表明:甲、乙两种树苗的成活率分别为85%,90%.
(1)若购买这两种树苗共用去21000元,则甲、乙两种树苗各购买多少株?
(2)若要使这批树苗的总成活率不低于88%,则甲种树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,使购买树苗的费用最低,并求出最低费用.
解方程: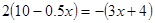
计算: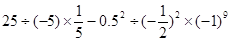
计算: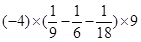
某个体户以每件80元的价格进了一种服装100件,用五天的时间售完.在销售过程中,发现由于每天销售的价格不同,所销售的件数就不一样(如图所示).
另外,每天的支出情况见下表:
| 日支出项目 |
房租 |
税收 |
员工工资 |
其他 |
| 日支出金额(元) |
100 |
60 |
90 |
30 |
根据图表提供的信息,回答下列问题:
(1)销售价是110元的这一天,卖了多少件?除去所有开支和进货成本,净赚了多少元?
(2)卖完100件这种服装后,除去5天的开支和进货的成本,共净赚了多少元?
你会数线段吗?
如图①线段AB ,即图中共有1条线段,1=
如图②线段AB上有1个点C,则图中共有3条线段,3=1+2=
如图③线段AB上有2个点C、D,则图中共有6条线段, 6=1+2+3=

思考问题:
(1)如果线段AB上有3个点则图中共有条线段;
(2)如果线段AB上有9个点则图中共有条线段;
(3)如果线段AB上有n个点则图中共有条线段(用含n的代数式来表示);