问题1:同学们已经体会到灵活运用乘法公式给整式乘法及多项式的因式分解带来的方便、快捷.相信通过下面材料的学习探究,会使你大开眼界并获得成功的喜悦.
例:用简便方法计算194×206.
解:194×206-(200-6)(200+6)①
=2002-62②
=39964
(1)例题求解过程中,从第①步到第②步的变形是利用(填乘法公式的名称);
(2)用简便方法计算:9×11×101.
问题2:对于形如x2+2xa+a2这样的二次三项式,可以用公式法将它分解成(x+a)2的形式.但对于二次三项式x2+2xa-3a2,就不能直接运用公式了.此时,我们可以在二次三项式x2+2xa-3a2中先加上一项a2,使它与x2+2xa的和成为一个完全平方式,再减去a2,整个式子的值不变,于是有:
x2+2xa-3a2=(a2+2ax+a2)-a2-3a2
=(x+a)2-4a2
=(x+a)2-(2a)2
=(x+3a)(x-a)
像这样,先添一适当项,使式中出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”,利用“配方法”,解决下列问题:
(1)分解因式:a2-6a+8;
(2)若x2-2xy+2y2+2y+1=0,求xy的值.
“保护生态环境,建设绿色家园”已经从理念变为人们的行动,苏州某地建立了绿色无公害蔬菜基地,现有甲、乙两种植户,他们种植了A、B两类蔬菜,两种植户种植的两类蔬菜的种植面积与总收入如下表:
说明:不同种植户种植的同类蔬菜每亩平均收入相等.
(1)求A、B两类蔬菜每亩平均收入各是多少元?
(2)另有某种植户准备租20亩地用来种植A、B两类蔬菜,为了使总收入不低于63000元,且种植A类蔬菜的面积多于种植B类蔬菜的面积(两类蔬菜的种植面积均为整数),求该种植户所有种植方案.
我们知道,等腰三角形的两个底角相等,即在△ABC中,∵AB=AC,∴∠B=∠C(如图①所示).请根据上述内容探究下面问题:
(1)如图②,已知在△ABC和△ADE中,AB=AC,AD=AE,∠CAB=∠DAE=90°,动点D在BC边上运动,试证明CD=BE且CD⊥BE.
(2)如图③,在(1)的条件下,若动点D在CB的延长线上运动,则CD与BE垂直吗?请在横线上直接写出结论,不必给出证明,答:_______.
(3)如图④,已知在△ABC和△ADE中,AB=AC,AD=AE,∠CAB=∠DAE=90°,动点D在△ABC内运动,试问CD⊥BE还成立吗?若成立,请给出证明过程.
(4)如图④,已知在△ABC和△ADE中,AB=AC,AD=AE,∠CAB=∠DAE=x°(90<x<180),点D在△ABC内,请在横线上直接写出直线CD与直线BE相交所成的锐角(用x的代数式表示).答:直线CD与直线BE相交所成的锐角______________.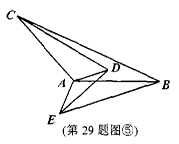
某电器经营业主计划购进一批同种型号的冷风扇和普通电风扇,若购进8台冷风扇和20台普通电风扇,需要资金17400元;若购进10台冷风扇和30台普通电风扇,需要资金22500元.
(1)求冷风扇和普通电风扇每台的采购价各是多少元?
(2)该经营业主计划购进这两种电器共70台,而可用于购买这两种电器的资金不超过30000元,根据市场行情,销售一台这样的冷风扇可获利200元,销售一台这样的普通电风扇可获利30元.该业主希望当这两种电器销售完时,所获得的利润不少于3500元,试问:该经营业主有哪几种进货方案,各种进货方案分别可获利多少元?
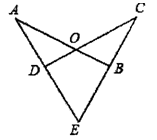
如图,已知线段AB、CD相交于点O,AD、CB的延长线交于点E,∠ODA=∠OBC,AD=CB,求证:AE=CE.