问题1:同学们已经体会到灵活运用乘法公式给整式乘法及多项式的因式分解带来的方便、快捷.相信通过下面材料的学习探究,会使你大开眼界并获得成功的喜悦.
例:用简便方法计算194×206.
解:194×206-(200-6)(200+6) ①
=2002-62 ②
=39964
(1)例题求解过程中,从第①步到第②步的变形是利用 (填乘法公式的名称);
(2)用简便方法计算:9×11×101.
问题2:对于形如x2+2xa+a2这样的二次三项式,可以用公式法将它分解成(x+a)2的形式.但对于二次三项式x2+2xa-3a2,就不能直接运用公式了.此时,我们可以在二次三项式x2+2xa-3a2中先加上一项a2,使它与x2+2xa的和成为一个完全平方式,再减去a2,整个式子的值不变,于是有:
x2+2xa-3a2=(a2+2ax+a2)-a2-3a2
=(x+a)2-4a2
=(x+a)2-(2a)2
=(x+3a)(x-a)
像这样,先添一适当项,使式中出现完全平方式,再减去这个项,使整个式子的值不变的方法称为“配方法”,利用“配方法”,解决下列问题:
(1)分解因式:a2-6a+8;
(2)若x2-2xy+2y2+2y+1=0,求xy的值.
某市第二届风筝节——“以鹞会友”活动于4月9日在西区公园举行.如图,广场上空有一风筝A,在地面上的B,C两点与点D在一条直线上.在点B和C分别测得风筝A的仰角∠ABD为45°,∠ACD为60°,又测得BC=20m.求风筝A离地面的高度.
(≈1.41,≈1.73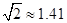 ,,结果精确到0.1米)
,,结果精确到0.1米)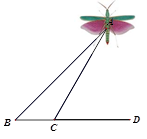
如图,在平面直角坐标系中,直线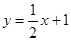 与抛物线
与抛物线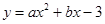 交于A,B两点,点A在
交于A,B两点,点A在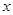 轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作
轴上,点B的纵坐标为3.点P是直线AB下方的抛物线上一动点(不与A,B重合),过点P作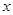 轴的垂线交直线AB与点C,作PD⊥AB于点D
轴的垂线交直线AB与点C,作PD⊥AB于点D
(1)求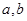 及
及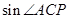 的值
的值
(2)设点P的横坐标为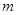
①用含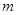 的代数式表示线段PD的长,并求出线段PD长的最大值;
的代数式表示线段PD的长,并求出线段PD长的最大值;
②连接PB,线段PC把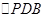 分成两个三角形,是否存在适合的
分成两个三角形,是否存在适合的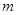 值,使这两个三角形的面积之比为9:10?若存在,直接写出
值,使这两个三角形的面积之比为9:10?若存在,直接写出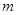 值;若不存在,说明理由.
值;若不存在,说明理由.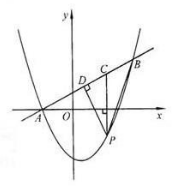
类比、转化、从特殊到一般等思想方法,在数学学习和研究中经常用到,如下是一个案例,请补充完整.
原题:如图1,在 中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若
中,点E是BC边上的中点,点F是线段AE上一点,BF的延长线交射线CD于点G,若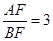 ,求
,求 的值。
的值。
(1)尝试探究
在图1中,过点E作 交BG于点H,则AB和EH的数量关系是,CG和EH的数量关系是,
交BG于点H,则AB和EH的数量关系是,CG和EH的数量关系是, 的值是
的值是
(2)类比延伸
如图2,在原题的条件下,若 则
则 的值是(用含
的值是(用含 的代数式表示),试写出解答过程。
的代数式表示),试写出解答过程。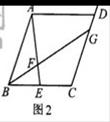
(3)拓展迁移
如图3,梯形ABCD中,DC∥AB,点E是BC延长线上一点,AE和BD相交于点F,若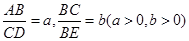 ,则
,则 的值是(用含
的值是(用含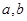 的代数式表示).
的代数式表示).
某中学计划购买A型和B型课桌凳共200套,经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,,且购买4套A型和6套B型课桌凳共需1820元。
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳的 ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
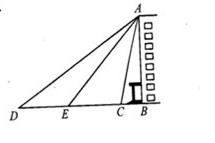
某宾馆为庆祝开业,在楼前悬挂了许多宣传条幅,如图所示,一条幅从楼顶A处放下,在楼前点C处拉直固定,小明为了测量此条幅的长度,他先在楼前D处测得楼顶A点的仰角为31°,再沿DB方向前进16米到达E处,测得点A的仰角为45°,已知点C到大厦的距离BC=7米,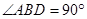 ,请根据以上数据求条幅的长度(结果保留整数.参考数据:
,请根据以上数据求条幅的长度(结果保留整数.参考数据: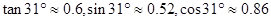 )
)