某市第二届风筝节——“以鹞会友”活动于4月9日在西区公园举行.如图，广场上空有一风筝A，在地面上的B,C两点与点D在一条直线上.在点B和C分别测得风筝A的仰角∠ABD为45°，∠ACD为60°,又测得BC=20m.求风筝A离地面的高度．
（≈1.41，≈1.73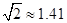
，，结果精确到0.1米）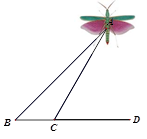
（本题12分）如图，在平面直角坐标系中，矩形ABCO的面积为15，边OA比OC大2．E为BC的中点，以OE为直径的⊙G交x轴于D点，过点D作DF⊥AE于点F．
（1）求OA、OC的长；
（2）求证：DF为⊙G的切线；
（3）小明在解答本题时，发现△AOE是等腰三角形．那么，直线BC上是否存在除点E以外的点P，使△AOP也是等腰三角形，如果存在，请直接写出所有符合题意的点P坐标．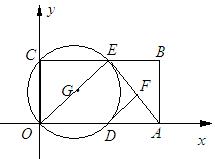
（本题10分）如图，⊙O的直径AB=4，点P是AB延长线上的一点，过点P作⊙O的切线，切点为C，连结AC．
（1）若∠CPA=30°，求PC的长；
（2）若点P在AB的延长线上运动，∠CPA的平分线交AC于点M．你认为∠CMP的大小是否发生变化？若变化，请说明理由；若不变化，请求出∠CMP的值．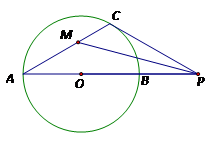
（本题10分）如图，P是双曲线
的一个分支上的一点，以点P为圆心，1个单位长度为半径作⊙P，设点P的坐标为（
，
）．
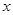（1）求当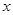为何值时，⊙P与直线
相切，并求点P的坐标．
（2）直接写出当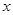为何值时，⊙P与直线相交、相离．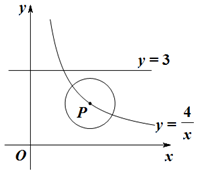
（本题10分）已知△ABC的一条边BC的长为5，另两边AB、AC的长是关于x的一元二次方程
的两个实数根．
（1）求证：无论
为何值时，方程总有两个不相等的实数根；
（2）当为何值时，△ABC是以BC为斜边的直角三角形；
（本题10分）已知AB为⊙O的直径，PA、PC是⊙O的切线，A、C为切点，∠BAC＝30°．①求∠P的度数；②若AB＝2，求PA的长．