今年我区为绿化行车道,计划购买甲、乙两种树苗共计n棵.设买甲种树苗x棵.有关甲、乙两种树苗的信息如图所示.
(1)当n=500时,
①根据信息填表(用含x代数式表示)
②如果购买甲、乙两种树苗共用25600元,那么甲、乙两种树苗各买了多少棵?
(2)要使这批树苗的成活率不低于92%,且使购买这两种树苗的总费用为26000元,求n的最大值.
先化简,再求值: ,其中,
,其中,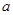 是方程
是方程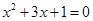 的根.
的根.
如图(1),我们将相同的两块含30°角的直角三角尺Rt△DEF与Rt△ABC叠合,使DE在AB上,DF过点C,已知AC=DE=6。将图(1)中的△DEF绕点D逆时针旋转(DF与AB不重合),使边DF、DE分别交AC、BC于点P、Q,如图(2)。
(1)求证:△CQD∽△APD
(2)连结PQ,设AP=x,求面积S△PCQ关于x的函数关系式;
(3)将图(1)中的△DEF 向左平移(A、D不重合),使边FD、FE分别交AC、BC于点M、N,如图(3),连结MN,试问△MCN面积是否存在最大值、如不存在,请说明理由;如存在请求出S△MCN 的最大值,
已知,如图,A,B分别在x轴和y轴上,且OA=2OB,直线y1=kx+b经过A点与抛物线y2=-x2+2x+3交于B,C两点,
(1)试求k,b的值及C点坐标;
(2)x取何值时y1,y2均随x的增大而增大;
(3)x取何值时y1>y2.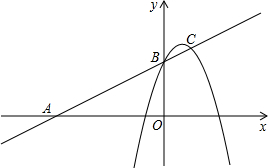
泰州新星电子科技公司积极应对世界金融危机,及时调整投资方向,瞄准光伏产业,建成了太阳能光伏电池生产线.由于新产品开发初期成本高,且市场占有率不高等因素的影响,产品投产上市一年来,公司经历了由初期的亏损到后来逐步盈利的过程(公司对经营的盈亏情况每月最后一天结算1次).公司累积获得的利润y(万元)与销售时间第x(月)之间的函数关系式(即前x个月的利润总和y与x之间的关系)对应的点都在如图所示的图象上.该图象从左至右,依次是线段OA、曲线AB和曲线BC,其中曲线AB为抛物线的一部分,点A为该抛物线的顶点,曲线BC为另一抛物线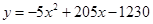 的一部分,且点A,B,C的横坐标分别为4,10,12
的一部分,且点A,B,C的横坐标分别为4,10,12
(1)求该公司累积获得的利润y(万元)与时间第x(月)之间的函数关系式;
(2)直接写出第x个月所获得S(万元)与时间x(月)之间的函数关系式(不需要写出计算过程);
(3)前12个月中,第几个月该公司所获得的利润最多?最多利润是多少万元?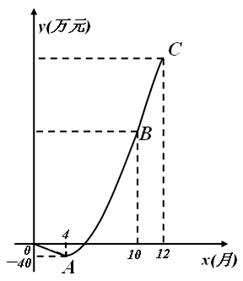
如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A.与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC.AD.BC之间的数量关系,并说明理由;
(3)若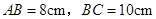 ,求大圆与小圆围成的圆环的面积.(结果保留π)
,求大圆与小圆围成的圆环的面积.(结果保留π)