如图(1),我们将相同的两块含30°角的直角三角尺Rt△DEF与Rt△ABC叠合,使DE在AB上,DF过点C,已知AC=DE=6。将图(1)中的△DEF绕点D逆时针旋转(DF与AB不重合),使边DF、DE分别交AC、BC于点P、Q,如图(2)。
(1)求证:△CQD∽△APD
(2)连结PQ,设AP=x,求面积S△PCQ关于x的函数关系式;
(3)将图(1)中的△DEF 向左平移(A、D不重合),使边FD、FE分别交AC、BC于点M、N,如图(3),连结MN,试问△MCN面积是否存在最大值、如不存在,请说明理由;如存在请求出S△MCN 的最大值,
如图,△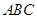 和△
和△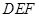 中,
中,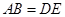 ,
,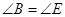 ,
,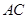 、
、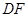 相交于点
相交于点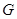 ,点
,点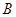 、
、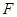 、
、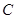 、
、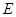 在同一直线上,且
在同一直线上,且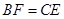 .求证:
.求证: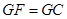 .
.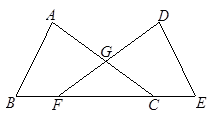
解方程: .
.
如图甲,四边形OABC的边OA、OC分别在x轴、y轴的正半轴上,顶点在B点的抛物线交x轴于点A、D,交y轴于点E,连接AB、AE、BE.已知tan∠CBE=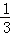 ,A(3,0),D(﹣1,0),E(0,3).
,A(3,0),D(﹣1,0),E(0,3).
(1)求抛物线的解析式及顶点B的坐标;
(2)求证:CB是△ABE外接圆的切线;
(3)试探究坐标轴上是否存在一点P,使以D、E、P为顶点的三角形与△ABE相似,若存在,直接写出点P的坐标;若不存在,请说明理由;
(4)设△AOE沿x轴正方向平移t个单位长度(0<t≤3)时,△AOE与△ABE重叠部分的面积为s,求s与t之间的函数关系式,并指出t的取值范围.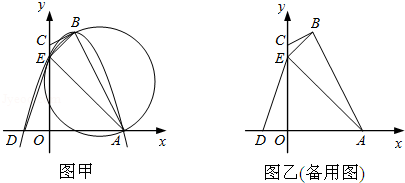
已知:y关于x的函数y=(k﹣1)x2﹣2kx+k+2的图象与x轴有交点.
(1)求k的取值范围;
(2)若x1,x2是函数图象与x轴两个交点的横坐标,且满足(k﹣1)x12+2kx2+k+2=4x1x2.
①求k的值;②当k≤x≤k+2时,请结合函数图象确定y的最大值和最大值.
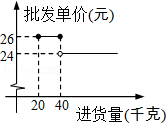
荆门市是著名的“鱼米之乡”.某水产经销商在荆门市长湖养殖场批发购进草鱼和乌鱼(俗称黑鱼)共75千克,且乌鱼的进货量大于40千克.已知草鱼的批发单价为8元/千克,乌鱼的批发单价与进货量的函数关系如图所示.
(1)请直接写出批发购进乌鱼所需总金额y(元)与进货量x(千克)之间的函数关系式;
(2)若经销商将购进的这批鱼当日零售,草鱼和乌鱼分别可卖出89%、95%,要使总零售量不低于进货量的93%,问该经销商应怎样安排进货,才能使进货费用最低?最低费用是多少?