如图所示的平面直角坐标系,在第Ⅰ象限内有平行于y轴的匀强电场,方向沿正方向;在第Ⅳ象限的正三角形区域内有匀强电场,方向垂直于平面向里,正三角形边长为,且边与轴平行。一质量为、电荷量为的粒子,从轴上的点,以大小为的速度沿轴正方向射入电场,通过电场后从轴上的点进入第Ⅳ象限,又经过磁场从轴上的某点进入第Ⅲ象限,且速度与轴负方向成45°角,不计粒子所受的重力。求:
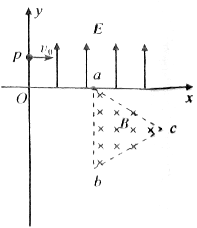
(1)电场强度的大小;
(2)粒子到达点时速度的大小和方向;
(3)区域内磁场的磁感应强度的最小值。
如图所示,光滑的金属导轨放在磁感应强度B=0.2T的匀强磁场中。平行导轨的宽度d=0.3m,定值电阻R=0.5。在外力F作用下,导体棒ab以v=20m/s的速度沿着导轨向左匀速运动。导体棒和导轨的电阻不计。求:
(1)通过R的感应电流大小;
(2)外力F的大小。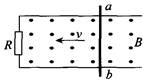
如图所示,质量为M=20kg的物体从光滑曲面上高度为h=0.8m处释放,到达底端时水平进入传送带,传送带由一电动机驱动着匀速向左转动,速率为3m/s。已知物体与传送带之间的动摩擦因素为0.1.物体冲上传送带后就撤走光滑曲面。
(1)若两皮带轮之间的距离是6m,物体将从哪一边离开传动带?(g=10m/s2)
(2)若皮带轮的距离足够大,从M滑上到离开传送带的整个过程中,由于M和传送带间的摩擦而产生了多少热量?电动机多做的总功又是多少?
如图滑板运动是一项惊险刺激的运动,深受青少年的喜爱。如图是滑板运动的轨道,AB和CD是一段圆弧形轨道,BC是一段长7m的水平轨道。一运动员从AB轨道上P点以6m/s的速度下滑,经BC轨道后冲上CD轨道,到Q点时速度减为零。已知运动员的质量50kg,h=1.4m,H=1.8m,不计圆弧轨道上的摩擦。求: (g=10m/s2)
(1)运动员第一次经过B点、C点时的速度各是多少?
(2) 运动员与BC轨道的动摩擦因数?
(3) 运动员最后停在BC轨道上何处?
竖直向上抛出质量为0.1kg的石头,石头上升过程中,空气阻力忽略不计,石头离手时的速度是20m/s.求:(g取10m/s2)
(1)石头离手时的动能;
(2)石头能够上升的最大高度;
(3)石头离地面15m高处的速度
额定功率为80kw的汽车在水平平直公路上行驶时最大速率可达20m/s,汽车质量为2t,如果汽车从静止开始做匀加速运动,设运动过程中阻力不变,加速度大小为2m/s2,求:
(1)汽车受阻力多大?
(2)3s末汽车的瞬时功率多大?
(3)汽车做匀加速运动的过程可以维持多长时间?