已知数列{an}的前n项和为Sn,且an是Sn与2的等差中项,数列{an}中,b1=1,点P(bn,bn+1)在直线x-y+2=0上.
(Ⅰ) 求数列{an},{bn}的通项公式an和bn;
(Ⅱ) 设cn=an•bn,求数列{cn}的前n项和Tn
已知 是同一平面内的三个向量,其中
是同一平面内的三个向量,其中
(1)若 ,且
,且 ,求:
,求: 的坐标;
的坐标;
(2)若 ,且
,且 与
与 垂直,求
垂直,求 与
与 的夹角;
的夹角;
如图, 是圆
是圆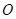 的直径,点
的直径,点 是圆
是圆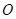 上异于
上异于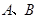 的点,直线
的点,直线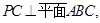
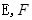 分别为
分别为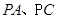 的中点。
的中点。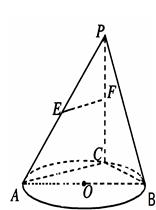
(1)记平面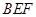 与平面
与平面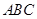 的交线为
的交线为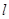 ,试判断
,试判断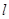 与平面
与平面 的位置关系,并加以说明;
的位置关系,并加以说明;
(2)设(1)中的直线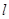 与圆
与圆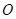 的另一个交点为
的另一个交点为 ,且点
,且点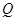 满足
满足 ,记直线
,记直线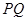
平面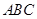 所成的角为
所成的角为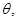 异面直线
异面直线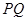 与
与 所成的锐角为
所成的锐角为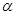 ,二面角
,二面角 的大小为
的大小为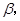
①求证: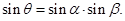
②当点 为弧
为弧 的中点时,
的中点时,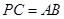 ,求直线
,求直线 与平面
与平面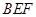 所成的角的正弦值。
所成的角的正弦值。
如图,在等腰直角三角形 中,
中, 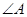 =900 ,
=900 , ="6,"
="6,"  分别是
分别是 ,
,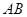 上的点,
上的点,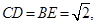
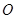 为
为 的中点.将
的中点.将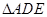 沿
沿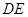 折起,得到如图所示的四棱椎
折起,得到如图所示的四棱椎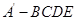 ,其中
,其中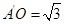


(1)证明: ;
;
(2)求二面角 的平面角的余弦值.
的平面角的余弦值.
如图所示,在三棱柱 中,
中,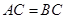 ,
,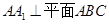 ,点
,点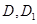 分别是
分别是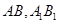 的中点.
的中点.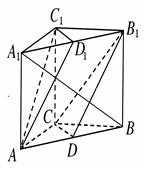
(1)求证:平面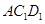 ∥平面
∥平面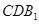 ;
;
(2)求证:平面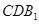 ⊥平面
⊥平面 ;
;
(3)若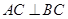 ,
, ,求异面直线
,求异面直线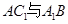 所成的角。
所成的角。
已知圆台的上、下底面半径分别是2、6,且侧面面积等于两底面面积之和。
(1)求该圆台的母线长;(2)求该圆台的体积。