将一颗质地均匀的正方体骰子(六个面的点数分别为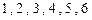 )先后抛掷两次,记第一次出现的点数为
)先后抛掷两次,记第一次出现的点数为 ,第二次出现的点数为
,第二次出现的点数为 .
.
(1)求事件“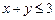 ”的概率;(2)求事件“
”的概率;(2)求事件“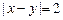 ”的概率.
”的概率.
在平面直角坐标系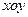 中,已知圆心在直线
中,已知圆心在直线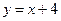 上,半径为
上,半径为 的圆C经过坐标原点O,椭圆
的圆C经过坐标原点O,椭圆 与圆C的一个交点到椭圆两焦点的距离之和为10.
与圆C的一个交点到椭圆两焦点的距离之和为10.
(1)求圆C的方程;
(2)若F为椭圆的右焦点,点P在圆C上,且满足 ,求点P
,求点P
某厂为适应市场需求,提高效益,特投入98万元引进先进设备,并马上投入生产,第一年需要的各种费用是12万元,从第二年开始,所需费用会比上一年增加4万元,而每年因引入该设备可获得的年利润为50万元。请你根据以上数据,解决下列问题:(1)引进该设备多少年后,开始盈利?(2)引进该设备若干年后,有两种处理方案:第一种:年平均盈利达到最大值时,以26万元的价格卖出;第二种:盈利总额达到最大值时,以8万元的价格卖出,哪种方案较为合算?请说明理由.
某城市有甲、乙、丙、丁4个旅游景点,一位客人游览这4个景点的概率都是0.6,且客人是否游览哪个景点互不影响.设 表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.
表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值.
(1)求 的分布列及数学期望;
的分布列及数学期望;
(2)记“函数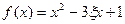 在区间
在区间 上单调递增”为事件A,求事件A的概率.
上单调递增”为事件A,求事件A的概率.
二阶矩阵M对应的变换将点(1,-1)与(-2,1)分别变换
成点(-1,-1)与(0,-2).
(1)求矩阵M;
(2)设直线l在变换M作用下得到了直线m:x-y=4,求l的方程