如图,在正方形 中, 为坐标原点,点 的坐标为 ,点 的坐标为 ,分别将线段 和 十等分,分点分别记为 和 ,连接 ,过 作 轴的垂线与 交于点 。

(1)求证:点
都在同一条抛物线上,并求抛物线
的方程;
(2)过点
作直线
与抛物线E交于不同的两点
, 若
与
的面积之比为4:1,求直线
的方程。
已知点A(– 2,0),B(2,0),动点P满足: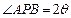 ,且
,且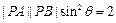 .
.
(1)求动点P的轨迹G的方程;
(2)过点B的直线l与轨迹G交于两点M、N.试问在x轴上是否存在定点C,使得 为常数.若存在,求出点C的坐标;若不存在,说明理由.
为常数.若存在,求出点C的坐标;若不存在,说明理由.
已知圆C: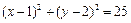 ,直线l:
,直线l: .
.
(1)证明:不论m取什么实数时,直线l与圆恒交于两点;
(2)求直线l被圆C截得的线段的最短长度以及此时直线l的方程.
数列{an}中,a1 = 1,当 时,其前n项和满足
时,其前n项和满足
(1)求Sn的表达式;
(2)设 ,数列{bn}的前n项和为Tn,求Tn.
,数列{bn}的前n项和为Tn,求Tn.
已知函数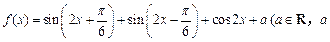 为常数).
为常数).
(1)求函数的最小正周期;
(2)求函数的单调递增区间;
(3)若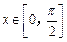 时,
时,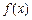 的最小值为– 2 ,求a的值.
的最小值为– 2 ,求a的值.
已知椭圆 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线 是抛物线
是抛物线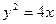 的一条切线.
的一条切线.
(Ⅰ)求椭圆的方程;
(Ⅱ)过点 的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ? 若存在,求点T坐标;若不存在,说明理由.
的动直线L交椭圆C于A、B两点.问:是否存在一个定点T,使得以AB为直径的圆恒过点T ? 若存在,求点T坐标;若不存在,说明理由.