设椭圆
的焦点在
轴上.
(Ⅰ)若椭圆
的焦距为1,求椭圆
的方程;
(Ⅱ)设
分别是椭圆的左、右焦点,
为椭圆
上第一象限内的点,直线
交
轴与点
,并且
,证明:当
变化时,点
在某定直线上.
已知数列{an}满足2an+1=an+an+2 (n∈N*),它的前n项和为Sn,且a3=-6,S6=-30.求数列{an}的前n项和的最小值.
已知函数 ,(1)求
,(1)求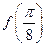 的值;(2)若
的值;(2)若 ,求
,求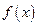 的值域.
的值域.

已知函数 ,其中
,其中 为实数.(1)若
为实数.(1)若 时,求曲线
时,求曲线 在点
在点 处的切线方程;(2)当
处的切线方程;(2)当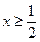 时,若关于
时,若关于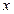 的不等式
的不等式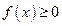 恒成立,试求
恒成立,试求 的取值范围.
的取值范围.
已知抛物线C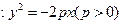 上横坐标为
上横坐标为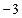 的一点,与其焦点的距离为4.(1)求
的一点,与其焦点的距离为4.(1)求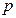 的值;(2)设动直线
的值;(2)设动直线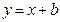 与抛物线C相交于A.B两点,问在直线
与抛物线C相交于A.B两点,问在直线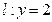 上是否存在与
上是否存在与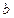 的取值无关的定点M,使得
的取值无关的定点M,使得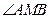 被直线
被直线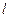 平分?若存在,求出点M的坐标;若不存在,说明理由.
平分?若存在,求出点M的坐标;若不存在,说明理由.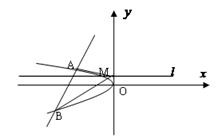
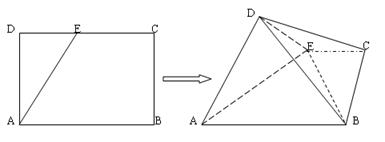
如图,在矩形ABCD中,AB=2,AD=1,E为CD的中点,将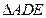 沿AE折起,使平面
沿AE折起,使平面 平面ABCE,得到几何体
平面ABCE,得到几何体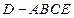 .(1)求证:
.(1)求证: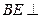 平面
平面 ;(2)求BD和平面
;(2)求BD和平面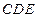 所成的角的正弦值.
所成的角的正弦值.