已知等差数列{an}的首项a1=1,公差d>0,且第2项、第5项、第14项分别为等比数列{bn}的第2项、第3项、第4项.
(1)求数列{an},{bn}的通项公式;
(2)设数列{cn}对n∈N*,均有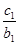 +
+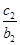 +…+
+…+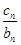 =an+1成立,求c1+c2+c3+…+c2014的值.
=an+1成立,求c1+c2+c3+…+c2014的值.
如图,在正方体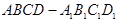 中,
中,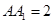 ,
,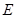 为
为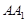 的中点,
的中点,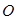 为
为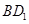 的中点.
的中点.
(1)求证:平面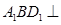 平面
平面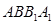 ;
;
(2)求证: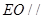 平面
平面 ;
;
(3)设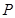 为正方体
为正方体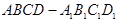 棱上一点,给出满足条件
棱上一点,给出满足条件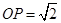 的点
的点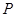 的个数,并说明理由.
的个数,并说明理由.
为了解某校学生的视力情况,现采用随机抽样的方式从该校的A,B两班中各抽5名学生进行视力检测.检测的数据如下:
A班5名学生的视力检测结果:4.3,5.1,4.6,4.1,4.9.
B班5名学生的视力检测结果:5.1,4.9,4.0,4.0,4.5.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?
(2)由数据判断哪个班的5名学生视力方差较大?(结论不要求证明)
(3)根据数据推断A班全班40名学生中有几名学生的视力大于4.6?
已知函数 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)当 时,求函数
时,求函数 的最大值和最小值.
的最大值和最小值.
在无穷数列 中,
中, ,对于任意
,对于任意 ,都有
,都有 ,
,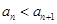 . 设
. 设 , 记使得
, 记使得 成立的
成立的 的最大值为
的最大值为 .
.
(1)设数列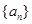 为1,3,5,7,
为1,3,5,7, ,写出
,写出 ,
, ,
,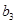 的值;
的值;
(2)若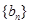 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列 ;
;
(3)设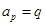 ,
, ,求
,求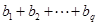 的值.(用
的值.(用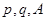 表示)
表示)
设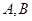 是椭圆
是椭圆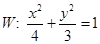 上不关于坐标轴对称的两个点,直线
上不关于坐标轴对称的两个点,直线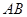 交
交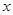 轴于点
轴于点 (与点
(与点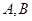 不重合),O为坐标原点.
不重合),O为坐标原点.
(1)如果点 是椭圆
是椭圆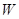 的右焦点,线段
的右焦点,线段 的中点在y轴上,求直线AB的方程;
的中点在y轴上,求直线AB的方程;
(2)设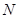 为
为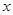 轴上一点,且
轴上一点,且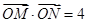 ,直线
,直线 与椭圆
与椭圆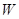 的另外一个交点为C,证明:点
的另外一个交点为C,证明:点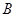 与点
与点 关于
关于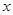 轴对称.
轴对称.