在平面直角坐标系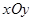 中,
中, 的边
的边 所在的直线方程是
所在的直线方程是 ,
,
(1)如果一束光线从原点 射出,经直线
射出,经直线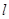 反射后,经过点
反射后,经过点 ,求反射后光线所在直线的方程;
,求反射后光线所在直线的方程;
(2)如果在 中,
中,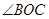 为直角,求
为直角,求 面积的最小值.
面积的最小值.
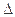 ABC中,a,b,c分别为内角A,B,C所对的边长,a=
ABC中,a,b,c分别为内角A,B,C所对的边长,a=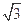 ,b=
,b=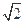 ,
,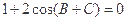 ,求边BC上的高.
,求边BC上的高.
(10分)已知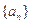 是公差不为零的等差数列,
是公差不为零的等差数列, 成等比数列.
成等比数列.
(Ⅰ)求数列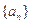 的通项;(Ⅱ)求数列
的通项;(Ⅱ)求数列 的前n项和
的前n项和
(本小题满分12分)
已知函数
(1)若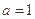 ,求曲线
,求曲线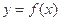 在点
在点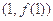 处的切线方程;
处的切线方程;
(2)若函数 在其定义域内为增函数,求
在其定义域内为增函数,求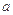 的取值范围;
的取值范围;
(3)在(2)的条件下,设函数 ,若在
,若在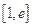 上至少存在一点
上至少存在一点 ,使得
,使得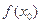
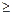
 成立,求实数
成立,求实数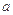 的取值范围.
的取值范围.
(本小题满分12分)
已知椭圆
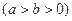 经过点
经过点 其离心率为
其离心率为
(1)求椭圆 的方程
的方程
(2)设直线 与椭圆
与椭圆 相交于A、B两点,以线段
相交于A、B两点,以线段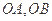 为邻边作平行四边形OAPB,其中顶点P在椭圆
为邻边作平行四边形OAPB,其中顶点P在椭圆 上,
上, 为坐标原点. 求
为坐标原点. 求 到直线
到直线 的距离的最小值.
的距离的最小值.
(本小题满分12分)
某校从高一年级期末考试的学生中抽出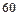 名学生,其成绩(均为整数)的频率分布直方图如图所示
名学生,其成绩(均为整数)的频率分布直方图如图所示
(1)估计这次考试的及格率(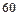 分及以上为及格);
分及以上为及格);
(2) 假设在[90,100]段的学生的成绩都不相同,且都在94分以上,现用简单随机抽样方法,从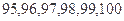 这
这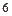 个数中任取
个数中任取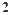 个数,求这
个数,求这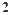 个数恰好是两个学生的成绩的概率.
个数恰好是两个学生的成绩的概率.