已知向量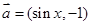 ,
,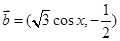 ,函数
,函数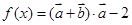 .
.
(1)求函数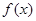 的最小正周期
的最小正周期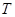 与值域;
与值域;
(2)已知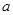 ,
,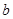 ,
,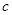 分别为
分别为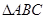 内角
内角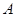 ,
, 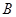 ,
,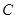 的对边,其中
的对边,其中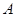 为锐角,
为锐角,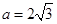 ,
, ,且
,且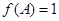 ,求
,求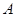 ,
,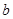 和
和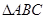 的面积
的面积 .
.
(本小题满分7分)选修4—5:不等式选讲
已知函数 .
.
(Ⅰ)求函数 的值域;
的值域;
(Ⅱ)设 ,试比较
,试比较 与
与 的大小.
的大小.
(本小题满分7分)《选修4-4:坐标系与参数方程》
已知曲线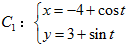 (
(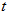 为参数),
为参数),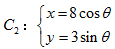 (
(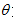 为参数).
为参数).
(Ⅰ)化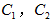 的方程为普通方程;
的方程为普通方程;
(Ⅱ)若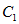 上的点对应的参数为
上的点对应的参数为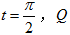 为
为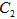 上的动点,求
上的动点,求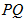 中点
中点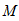 到直线
到直线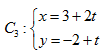 (
(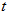 为参数)距离的最小值.
为参数)距离的最小值.
(本小题满分7分)选修4—2:矩阵与变换
在平面直角坐标系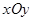 中,把矩阵
中,把矩阵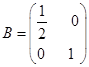 确定的压缩变换
确定的压缩变换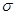 与矩阵
与矩阵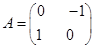 确定的旋转变换
确定的旋转变换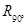 进行复合,得到复合变换
进行复合,得到复合变换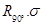 .
.
(Ⅰ)求复合变换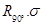 的坐标变换公式;
的坐标变换公式;
(Ⅱ)求圆C:x2+ y2 =1在复合变换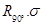 的作用下所得曲线
的作用下所得曲线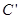 的方程.
的方程.
(本小题满分14分)若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其定义域上的任意实数
对其定义域上的任意实数 分别满足:
分别满足: 和
和 ,则称直线
,则称直线 为
为 和
和 的“隔离直线”.已知
的“隔离直线”.已知 ,
, 为自然对数的底数).
为自然对数的底数).
(1)求 的极值;
的极值;
(2)函数 和
和 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.