(本小题满分7分)《选修4-4:坐标系与参数方程》
已知曲线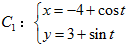 (
(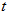 为参数),
为参数),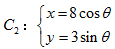 (
(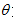 为参数).
为参数).
(Ⅰ)化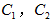 的方程为普通方程;
的方程为普通方程;
(Ⅱ)若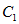 上的点对应的参数为
上的点对应的参数为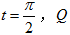 为
为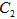 上的动点,求
上的动点,求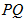 中点
中点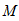 到直线
到直线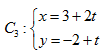 (
(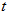 为参数)距离的最小值.
为参数)距离的最小值.
(本题满分13分)
已知直线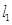 :
: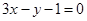 ,
, :
: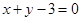 ,求:
,求:
(1)直线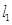 与
与 的交点
的交点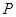 的坐标;(2)过点
的坐标;(2)过点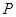 且与
且与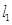 垂直的直线方程.
垂直的直线方程.
(本小题满分13分)在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.
(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1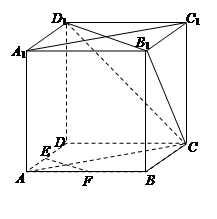
(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分)如图1,在四边形 中,点C(1,3).(1)求OC所在直线的斜率;
中,点C(1,3).(1)求OC所在直线的斜率;
(2)过点C做CD⊥AB于点D,求CD所在直线的方程.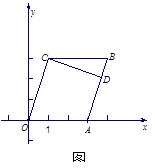
(本小题满分14分)
已知抛物线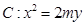
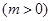 和直线
和直线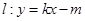 没有公共点(其中
没有公共点(其中 、
、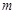 为常数),动点
为常数),动点 是直线
是直线 上的任意一点,过
上的任意一点,过 点引抛物线
点引抛物线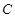 的两条切线,切点分别为
的两条切线,切点分别为 、
、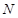 ,且直线
,且直线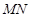 恒过点
恒过点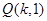 .
.
(1)求抛物线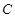 的方程;
的方程;
(2)已知 点为原点,连结
点为原点,连结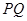 交抛物线
交抛物线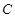 于
于 、
、 两点,
两点,
证明: .
.
(本小题满分13分)
已知函数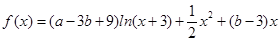 .
.
(1)当 且
且 ,
, 时,试用含
时,试用含 的式子表示
的式子表示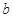 ,并讨论
,并讨论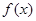 的单调区间;
的单调区间;
(2)若 有零点,
有零点, ,且对函数定义域内一切满足
,且对函数定义域内一切满足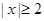 的实数
的实数 有
有 .
.
①求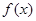 的表达式;
的表达式;
②当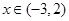 时,求函数
时,求函数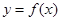 的图象与函数
的图象与函数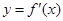 的图象的交点坐标.
的图象的交点坐标.