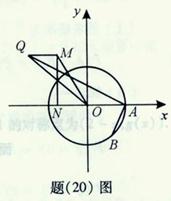
(本小题满分14分)
已知抛物线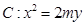
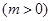 和直线
和直线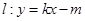 没有公共点(其中
没有公共点(其中 、
、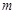 为常数),动点
为常数),动点 是直线
是直线 上的任意一点,过
上的任意一点,过 点引抛物线
点引抛物线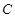 的两条切线,切点分别为
的两条切线,切点分别为 、
、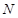 ,且直线
,且直线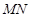 恒过点
恒过点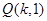 .
.
(1)求抛物线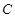 的方程;
的方程;
(2)已知 点为原点,连结
点为原点,连结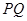 交抛物线
交抛物线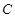 于
于 、
、 两点,
两点,
证明: .
.
(本小题满分12分)
已知与曲线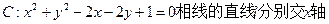 、y轴于
、y轴于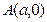 、
、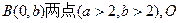 为原点。
为原点。
(1)求证: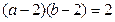 ;
;
(2)求线段AB中点的轨迹方程;
(3)求△AOB面积的最小值。
(文科)已知抛物线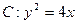 的准线与
的准线与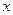 轴交于
轴交于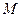 点,
点,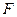 为抛物线
为抛物线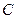 的焦点,过
的焦点,过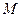 点斜率为
点斜率为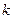 的直线与抛物线
的直线与抛物线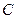 交于
交于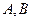 两点。
两点。
(1)若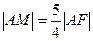 ,求
,求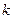 的值;
的值;
(2)是否存在这样的 ,使得抛物线
,使得抛物线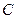 上总存在点
上总存在点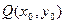 满足
满足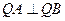 ,若存在,求
,若存在,求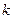 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
(13分)(理科)已知双曲线 与椭圆
与椭圆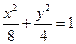 有公共焦点,且以抛物线
有公共焦点,且以抛物线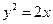 的准线为双曲线
的准线为双曲线 的一条准线.动直线
的一条准线.动直线 过双曲线
过双曲线 的右焦点
的右焦点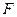 且与双曲线的右支交于
且与双曲线的右支交于 两点.
两点.
(1)求双曲线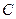 的方程;
的方程;
(2)无论直线 绕点
绕点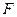 怎样转动,在双曲线
怎样转动,在双曲线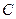 上是否总存在定点
上是否总存在定点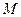 ,使
,使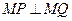 恒成立?若存在,求出点
恒成立?若存在,求出点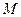 的坐标,若不存在,请说明理由.
的坐标,若不存在,请说明理由.
(文科)已知双曲线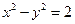 的右焦点为
的右焦点为 ,过点
,过点 的动直线与双曲线相交于
的动直线与双曲线相交于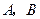 两点,点
两点,点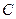 的坐标是
的坐标是 .
.
(I)证明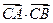 为常数;
为常数;
(II)若动点 满足
满足 (其中
(其中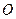 为坐标原点),求点
为坐标原点),求点 的轨迹方程.
的轨迹方程.
(理科)已知以原点 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为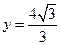 ,离心率
,离心率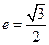 ,
,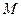 是椭圆上的动点.
是椭圆上的动点.
(1)若点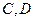 的坐标分别是
的坐标分别是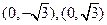 ,求
,求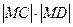 的最大值;
的最大值;
(2)如图,点 的坐标为
的坐标为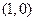 ,
, 是圆
是圆 上的点,点
上的点,点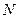 是点
是点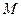 在
在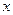 轴上的射影,点
轴上的射影,点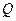 满足条件:
满足条件: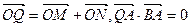 ,求线段
,求线段 的中点
的中点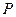 的轨迹方程.
的轨迹方程.