某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动,分别由李老师和张老师负责,已知该系共有 位学生,每次活动均需该系 位学生参加( 和 都是固定的正整数).假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系 位学生,且所发信息都能收到.记该系收到李老师或张老师所发活动通知信息的学生人数为 .
(Ⅰ)求该系学生甲收到李老师或张老师所发活动通知信息的概率;
(Ⅱ)求使
取得最大值的整数
.
已知命题
 ,满足
,满足 ,命题
,命题

 ,方程
,方程 都表示焦点在
都表示焦点在 轴上的椭圆.若命题
轴上的椭圆.若命题 为真命题,
为真命题, 为假命题,求
为假命题,求 实数
实数 的取值范围
的取值范围
在圆
 上任取一点
上任取一点 ,过点
,过点 作
作 轴的垂线段
轴的垂线段 ,
, 为垂足.当点
为垂足.当点 在圆上运动时,线段
在圆上运动时,线段 的中点
的中点 形成轨迹
形成轨迹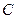 .
.
(1)求轨迹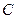 的方程;
的方程;
(2)若直线 与曲线
与曲线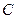 交于
交于 两点,
两点, 为曲线
为曲线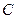 上一动点,求
上一动点,求 面积的最大值
面积的最大值
如图,设 点是圆
点是圆 上的动点,过点
上的动点,过点
 作圆
作圆 的两条切线,切点分别为
的两条切线,切点分别为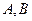 ,切线
,切线 分别交
分别交 轴于
轴于 两点.
两点.
(1)求四边形 面积的最小值;
面积的最小值;
(2)是否存在点 ,使得线段
,使得线段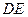 被圆
被圆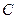 在点
在点 处的切线平分?若存在,求出点
处的切线平分?若存在,求出点 的纵坐标
的纵坐标 ;若不存在,说明理由.
;若不存在,说明理由.
如图,在平行四边形 中,
中, ,
, ,
, 为线段
为线段 的中线,将△
的中线,将△ 沿
沿 直线
直线 翻折成△
翻折成△ ,使平面
,使平面 ⊥平面
⊥平面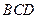 ,
,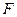 为线
为线 段
段 的中点.
的中点.
(1)求证: ∥平面
∥平面 ;
;
(2)设 为线段
为线段 的中点,求直线
的中点,求直线 与平面
与平面 所成角的余弦值.
所成角的余弦值.
已知一隧道的截面 是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有
是一个半椭圆面(如图所示),要保证车辆正常通行,车顶离隧道顶部至少要有 米的距离,现有一货车,车宽
米的距离,现有一货车,车宽 米,车高
米,车高 米.
米.
(1)若此隧道为单向通行,经测量隧道的跨度是 米,则应如何设计隧道才能保证此货车正常通行?
米,则应如何设计隧道才能保证此货车正常通行?
(2)圆可以看作是长轴短轴相等的特殊椭圆,类比圆面积公式,
请你推测椭圆 的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?
的面积公式.并问,当隧道为双向通行(车道间的距离忽略不记)时,要使此货车安全通过,应如何设计隧道,才会使同等隧道长度下开凿的土方量最小?