如图①,在等腰直角三角形
中,
,
,
分别是
上的点,
,
为
的中点.将
沿
折起,得到如图②所示的四棱锥
,其中
.
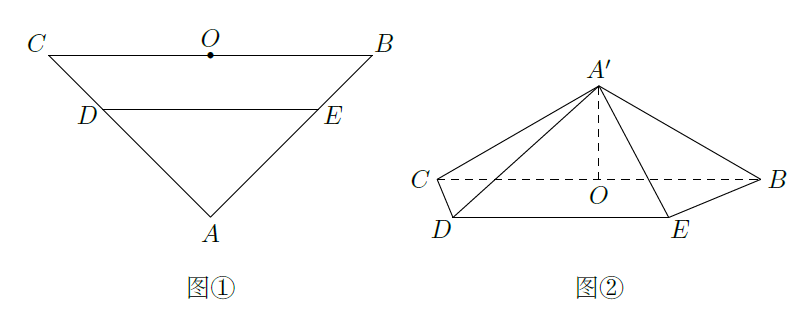
(Ⅰ) 证明:
;
(Ⅱ) 求二面角
的平面角的余弦值.
(本小题满分12分)
已知集合
(Ⅰ)求:A∪B;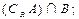
(Ⅱ)若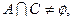 求a的取值范围.
求a的取值范围.
(本小题满分14分)
已知点 、
、 ,(
,( )是曲线C上的两点,点
)是曲线C上的两点,点 、
、 关于
关于 轴对称,直线
轴对称,直线 、
、 分别交
分别交 轴于点
轴于点 和点
和点 ,
,
(Ⅰ)用 、
、 、
、 、
、 分别表示
分别表示 和
和 ;
;
(Ⅱ)某同学发现,当曲线C的方程为: 时,
时, 是一个定值与点
是一个定值与点 、
、 、
、 的位置无关;请你试探究当曲线C的方程为:
的位置无关;请你试探究当曲线C的方程为: 时,
时,  的值是否也与点M、N、P的位置无关;
的值是否也与点M、N、P的位置无关;
(Ⅲ)类比(Ⅱ)的探究过程,当曲线C的方程为 时,探究
时,探究 与
与 经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).
经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).
(本小题满分14分)
已知中心在坐标轴原点O的椭圆C经过点A(1,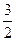 ),且点F(-1,0)为其左焦点.
),且点F(-1,0)为其左焦点.
(I)求椭圆C的离心率;
(II)试判断以AF为直径的圆与以椭圆长轴为直径的圆的位置关系,并说明理由.
(本小题满分13分)
设命题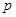 :对任意实数
:对任意实数 ,不等式
,不等式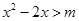 恒成立;命题
恒成立;命题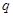 :方程
:方程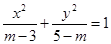 表示焦点在
表示焦点在 轴上的双曲线.
轴上的双曲线.
(I)若命题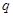 为真命题,求实数
为真命题,求实数 的取值范围;
的取值范围;
(II)若命题“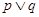 ”为真命题,且“
”为真命题,且“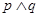 ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
(本小题满分13分)
已知抛物线 的顶点在原点,焦点为
的顶点在原点,焦点为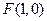 ,且过点
,且过点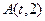 .
.
(1)求t的值;
(2)若直线 与抛物线
与抛物线 只有一个公共点,求实数
只有一个公共点,求实数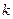 的值.
的值.