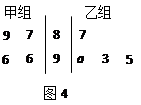设数列
的前
项和为
.已知
.
(Ⅰ) 求
的值;
(Ⅱ) 求数列
的通项公式;
(Ⅲ) 证明:对一切正整数
,有
.
.(本小题满分14分)
设函数 (
(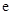 为自然对数的底数),
为自然对数的底数),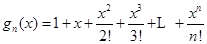 (
(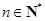 ).
).
(1)证明:
 ;
;
(2)当 时,比较
时,比较 与
与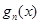 的大小,并说明理由;
的大小,并说明理由;
(3)证明: (
(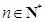 ).
).
(本小题满分14分)
已知椭圆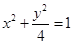 的左,右两个顶点分别为
的左,右两个顶点分别为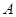 、
、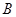 .曲线
.曲线 是以
是以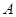 、
、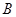 两点为顶点,离心率为
两点为顶点,离心率为 的双曲线.设点
的双曲线.设点 在第一象限且在曲线
在第一象限且在曲线 上,直线
上,直线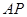 与椭圆相交于另一点
与椭圆相交于另一点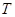 .
.
(1)求曲线 的方程;
的方程;
(2)设 、
、 两点的横坐标分别为
两点的横坐标分别为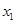 、
、 ,证明:
,证明: ;
;
(3)设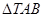 与
与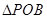 (其中
(其中 为坐标原点)的面积分别为
为坐标原点)的面积分别为 与
与 ,且
,且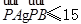 ,求
,求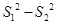 的取值范围.
的取值范围.
(本小题满分14分)
等比数列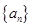 的各项均为正数,
的各项均为正数,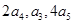 成等差数列,且
成等差数列,且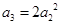 .
.
(1)求数列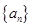 的通项公式;
的通项公式;
(2)设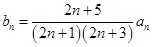 ,求数列
,求数列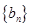 的前
的前 项和
项和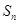 .
.
(本小题满分14分)
如图5所示,在三棱锥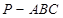 中,
中,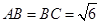 ,平面
,平面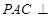 平面
平面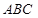 ,
,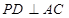 于点
于点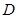 ,
, 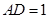 ,
,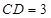 ,
, .
.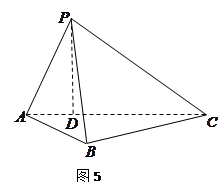
(1)证明△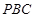 为直角三角形;
为直角三角形;
(2)求直线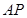 与平面
与平面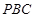 所成角的正弦值
所成角的正弦值
.(本小题满分12分)
如图4所示的茎叶图记录了甲、乙两个小组(每小组4人)在期末考试中
的数学成绩.乙组记录中有一个数据模糊,无法确认,在图中以 表示.
表示.
已知甲、乙两个小组的数学成绩的平均分相同.
(1)求 的值;
的值;
(2)求乙组四名同学数学成绩的方差;
(3)分别从甲、乙两组同学中各随机选取一名同学,记这两名同学数学
成绩之差的绝对值为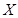 ,求随机变量
,求随机变量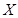 的分布列和均值(数学期望).
的分布列和均值(数学期望).