(本小题满分10分)选修4—4;坐标系与参数方程
已知直线 (
( 为参数),
为参数), .
.
(1)当 时,求
时,求 与
与 的交点坐标;
的交点坐标;
(2)以坐标原点 为圆心的圆与
为圆心的圆与 相切,切点为
相切,切点为 ,
, 为
为 的中点,当
的中点,当 变化时,求
变化时,求 点的轨迹的参数方程,并指出它是什么曲线.
点的轨迹的参数方程,并指出它是什么曲线.
已知函数 .
.
(1)求函数 的定义域;
的定义域;
(2)判定函数 的奇偶性,并加以证明;
的奇偶性,并加以证明;
(3)判定 的单调性,并求不等式
的单调性,并求不等式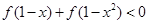 的解集.
的解集.
设函数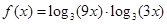 ,且
,且 .
.
(1)求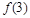 的值;
的值;
(2)若令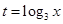 ,求
,求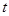 取值范围;
取值范围;
(3)将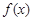 表示成以
表示成以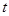 (
(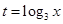 )为自变量的函数,并由此,求函数
)为自变量的函数,并由此,求函数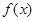 的最大值与最小值及与之对应的x的值.
的最大值与最小值及与之对应的x的值.
已知函数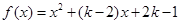 .
.
(1)若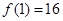 ,函数
,函数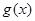 是R上的奇函数,当
是R上的奇函数,当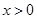 时
时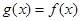 ,(i)求实数
,(i)求实数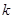 与
与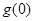
的值;(ii)当 时,求
时,求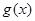 的解析式;
的解析式;
(2)若方程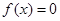 的两根中,一根属于区间
的两根中,一根属于区间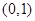 ,另一根属于区间
,另一根属于区间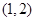 ,求实数
,求实数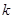 的取 值范围.
的取 值范围.
记关于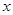 的不等式
的不等式 的解集为
的解集为 ,不等式
,不等式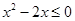 的解集为
的解集为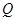 .
.
(1)若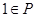 ,求实数
,求实数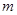 的取值范围;
的取值范围;
(2)若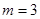 ,求集合
,求集合 ;
;
(3)若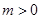 且
且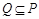 ,求
,求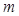 的取值范围.
的取值范围.
一袋中有6个黑球,4个白球.
(1)依次取出3个球,不放回,已知第一次取出的是白球,求第三次取到黑球的概率;
(2)有放回地依次取出3球,已知第一次取的是白球,求第三次取到黑球的概率;
(3)有放回地依次取出3球,求取到白球个数X的分布列、期望和方差.