某种项目的射击比赛,开始时在距目标100m处射击,如果命中记3分,且停止射击;若第一次射击未命中,可以进行第二次射击,但目标已在150m处,这时命中记2分,且停止射击;若第二次仍未命中,还可以进行第三次射击,此时目标已在200m处,若第三次命中则记1分,并停止射击;若三次都未命中,则记0分.已知射手甲在100m处击中目标的概率为 ,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
,他的命中率与目标的距离的平方成反比,且各次射击都是独立的.
(1)求这位射手在三次射击中命中目标的概率;
(2)求这位射手在这次射击比赛中得分的均值.
 为等腰直角三角形,
为等腰直角三角形, ,
, ,
, 、
、 分别是边
分别是边 和
和 的中点,现将
的中点,现将 沿
沿 折起,使面
折起,使面
 面
面 ,
, 、
、 分别是边
分别是边 和
和 的中点,平面
的中点,平面 与
与 、
、 分别交于
分别交于 、
、 两点.
两点.
(Ⅰ)求证:

 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
为了增强环保意识,我校从男生中随机抽取了60人,从女生中随机抽取了50人参加环保知识测试,统计数据如下表所示:
| 优秀 |
非优秀 |
总计 |
|
| 男生 |
40 |
20 |
60 |
| 女生 |
20 |
30 |
50 |
| 总计 |
60 |
50 |
110 |
(Ⅰ)试判断是否有99%的把握认为环保知识是否优秀与性别有关;
(Ⅱ)为参加市里举办的环保知识竞赛,学校举办预选赛,已知在环保测试中优秀的同学通过预选赛的概率为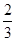 ,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量
,现在环保测试中优秀的同学中选3人参加预选赛,若随机变量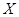 表示这3人中通过预选赛的人数,求
表示这3人中通过预选赛的人数,求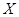 的分布列与数学期望.
的分布列与数学期望.
 |
0.500 |
0.400 |
0.100 |
0.010 |
0.001 |
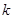 |
0.455 |
0.708 |
2.706 |
6.635 |
10.828 |
附: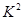 =
=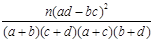
已知数列 的前
的前 项和为
项和为 ,且满足
,且满足 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,
, ,且数列
,且数列 的前
的前 项和为
项和为 ,求
,求 的取值范围.
的取值范围.
已知函数 .
.
(1)当 时,求函数
时,求函数 在
在 上的值域;
上的值域;
(2)若对任意 ,总有
,总有 成立,求实数
成立,求实数 的取值范围.
的取值范围.
已知二次函数
(1)若函数在区间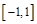 上存在零点,求实数
上存在零点,求实数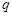 的取值范围;
的取值范围;
(2)问:是否存在常数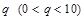 ,使得当
,使得当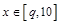 时,
时, 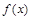 的最小值为
的最小值为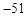 ?若存在,求出
?若存在,求出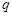 的值,若不存在,说明理由。
的值,若不存在,说明理由。