设
是首项为
，公差为
的等差数列（
），
是前
项和. 记
，
，其中
为实数.
（1）若
，且
成等比数列，证明：
；
（2）若
是等差数列，证明
.
某品牌的汽车4S店，对最近100位采用分期付款的购车者进行统计，统计结果如右表所示：
| 付款方式 |
分l期 |
分2期 |
分3期 |
分4期 |
分5期 |
| 频数 |
已知分3期付款的频率为0．2，4S店经销一辆该品牌的汽车，顾客分1期付款，其利润为1万元；分2期或3期付款其利润为1.5万元；分4期或5期付款，其利润为2万元．用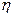
表示经销一辆汽车的利润．
（Ⅰ）求上表中a，b的值；
（Ⅱ）若以频率作为概率，求事件A：“购买该品牌汽车的3位顾客中，至多有l位采用3期付款”的概率P（A）；
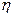（Ⅲ）求的分布列及数学期望
．
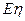（本
小题满分12分）在直三棱柱
ABC—A1B1C1中，CA=CB=CC1=2，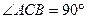
，E、F分别是BA、BC的中点，G是AA1上一点，且
（Ⅰ）确定点G的位置；
（Ⅱ）求直线AC1与平面EFG所成角θ的大小．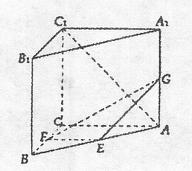
（本小题满分12分）设数列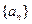
的前n项和为
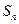，且
（Ⅰ）设
，求证：数列
是等比数列；
（Ⅱ）求数列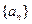的通项公式．
（本小题满分12分）
已知数列
（I）求
的通项公式；
（II）求证：
（本小题满分12分）
已知A、B是抛物线
上的两点，O是抛物线
的顶点，OA⊥OB。
（I）求证：直线AB过定点M（4，0）；
（II）设弦AB的中点为
P，求点P到直线
的距离的最小值。