圆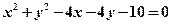 上至少有三个不同的点到直线
上至少有三个不同的点到直线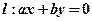 的距离为
的距离为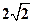 ,则直线
,则直线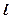 的倾斜角的取值范围是()
的倾斜角的取值范围是()
A.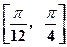 |
B.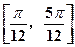 |
C.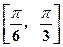 |
D.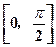 |
已知数列 的前
的前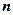 项和为
项和为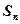 ,则关于
,则关于 的命题(其中
的命题(其中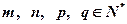 )。
)。
①若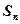 是关于
是关于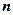 的二次函数,则
的二次函数,则 是等差数列;
是等差数列;
② ;
;
③若 是等比数列,且
是等比数列,且 ,则
,则 ;
;
④若 是等差数列,且
是等差数列,且 ,则
,则 ;
;
⑤若 是等差数列,则
是等差数列,则 。其中正确的有()个。
。其中正确的有()个。
| A.2 | B.3 | C.4 | D.5 |
对 ,记
,记 ,函数
,函数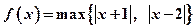
 的最小值是()
的最小值是()
| A.0 | B.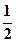 |
C.1 | D.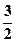 |
在一次实验中,测得(x,y)的四组值分别为(1,2),(2,3),(3,4),(4,5),则y与x的线性回归方程可能是()
A. |
B. |
C. |
D. |
若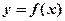 是定义在
是定义在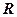 上的函数,则
上的函数,则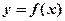 为奇函数的一个充要条件为()
为奇函数的一个充要条件为()
A.存在某个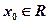 ,使得 ,使得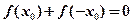 |
B.对任意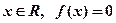 都成立 都成立 |
C.对任意的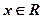 ,都有 ,都有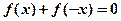 成立 成立 |
D.f(x)=0 |