如图所示，两根平行的导轨处于同一水平面内，相距为L．导轨左端用阻值为R的电阻相连，导轨的电阻不计。导轨上跨接一质量为m、电阻为r的金属杆，金属杆与导轨之间的动摩擦因数为μ．整个装置放在竖直向下的匀强磁场中，磁感应强度为B，磁场宽度为S1．现对杆施加一水平向右的恒定拉力F，使它由静止开始进入磁场区域，当金属杆离开磁场时立即将拉力F撤去，金属杆继续运动了一段距离后停止在导轨上。已知重力加速度为g．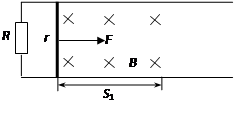
（1）若金属杆在离开磁场前就做匀速直线运动，求匀速运动的速度；
（2）金属杆运动过程，通过电阻R的电量是多少？
（3）若金属杆离开磁场继续运动了S2后停止在导轨上。金属杆运动过程，电阻R产生的热量是多少？
一半径为R的雨伞绕伞柄以角速度ω匀速转动，如图所示，伞边缘距地面高为h，甩出的水滴做平抛运动，在地面上形成一个圆，求此圆半径r为多少？ 
汽车质量为m，汽车与地面间的最大静摩擦力为车对地面压力的k倍，欲使汽车转弯时不打滑：
（1）如果弯道是一水平的半径为R的圆弧，汽车在弯道处行驶的最大速度为多少？
（2）如果弯道是一倾角为θ、半径为R的圆弧，最理想（即汽车不受摩擦力）的速度为多少？
如图所示，在距地面高为H＝45 m处，有一小球A以初速度V0＝10 m/s水平
抛出，与此同时，在A的正下方有一物块B也以相同的初速度V0同方向滑出，B与地面间
的动摩擦因数为μ＝0.5，A、B均可看做质点，空气阻力不计。求：
（1）A球从抛出到落地的时间；
（2）A球从抛出到落地这段时间内的水平位移；
（3）A球落地时，A、B之间的距离。
如图甲，在水平桌面上固定着两根相距0.2m,相互平行的无电阻轨道P和轨道一端固定一根电阻为0.0l Ω的导体棒a，轨道上横置一根质量为40g、电阻为0.0lΩ的金属棒b，两棒相距0.2m．该轨道平面处在磁感应强度大小可以调节的竖直向上的匀强磁场中．开始时，磁感应强度B0="0.10" T(设棒与轨道间的最大静摩擦力和滑动摩擦力相等，g取10 m/s2)
（1）若从t=0开始，磁感应强度B随时间t按图乙中图象所示的规律变化，求在金属棒b开始运动前，这个装置释放的热量是多少?
（2）若保持磁感应强度B0的大小不变，从t=0时刻开始，给b棒施加一个水平向右的拉力，使它做匀加速直线运动．此拉力F的大小随时间t变化关系如图丙所示．求匀加速运动的加速度及b棒与导轨间的滑动摩擦力．
某发电站的输出功率为104 kW，输出电压为4 kV，通过理想变压器升压后向80 km远处用户供电，在用户区再用降压器把电压降为220V供用户使用。已知输电线的电阻率为ρ＝2.4×10－8Ω·m，导线横截面积为1.5×10－4 m2，输电线路损失的功率为输出功率的4%，求：
(1)升压变压器的输出电压．
(2)输电线路上的电压损失．
(3) 降压器原、副线圈的匝数比．