为了降低潜艇噪音,提高其前进速度,可用电磁推进器替代螺旋桨。潜艇下方有左、右两组推进器,每组由6个相同的用绝缘材料制成的直线通道推进器构成,其原理示意图如下。在直线通道内充满电阻率的海水,通道中a的空间内,存在由超导线圈产生的匀强磁场,其磁感应强度、方向垂直通道侧面向外。磁场区域上、下方各有的金属板、,当其与推进器专用直流电源相连后,在两板之间的海水中产生了从到,大小恒为的电流,设电流只存在于磁场区域。不计电源内阻及导线电阻,海水密度。

(1)求一个直线通道推进器内磁场对通电海水的作用力大小,并判断其方向。
(2)在不改变潜艇结构的前提下,简述潜艇如何转弯?如何倒车?
(3)当潜艇以恒定速度前进时,海水在出口处相对于推进器的速度,思考专用直流电源所提供的电功率如何分配,求出相应功率的大小。
一束电子流在经U=5 000 V的加速电压加速后,在距两极板等距离处垂直进入平行板间的匀强电场,如图所示.若两板间距d=1.0 cm,板长l=5.0 cm,那么要使电子能从平行板间飞出,两个极板上最多能加多大电压?
如图所示的匀强电场中,有a、b、c三点,ab=5cm,bc=12cm,其中ab沿电场方向,bc和电场方向成60°角,一电子(其电荷量为e=1.6×10-19C)从a移到b电场力做功为Wab=3.2×10-18J求: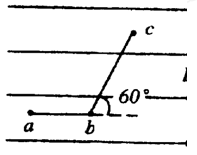
(1)匀强电场的场强大小及方向。
(2)电子从b移到c,电场力对它做功。
(3)设φa=0,则电子在c点的电势能为多少?
(4)a、c两点的电势差等于多少?
有一起重机用的是直流电动机,如图14所示,其内阻r=0.8Ω,线路电阻R=10Ω,电源电压U=150V,伏特表的示数为110V,求:
(1)通过电动机的电流.
(2)输入到电动机的功率P入.
(3)电动机的发热功率Pr,电动机输出的机械功率.
如图所示,M、N是水平放置的一对正对平行金属板,其中M板中央有一小孔O,板间存在竖直向上的匀强电场,AB是一根长为9L的轻质绝缘细杆,在杆上等间距地固定着10个完全相同的带电小球(小球直径略小于孔),每个小球带电荷量为q,质量为m,相邻小球间的距离为L,小球可视为质点,不考虑带电小球之间库仑力.现将最下端的小球置于O处,然后将AB由静止释放,AB在运动过程中始终保持竖直,经观察发现,在第二个小球进入电场到第三个小球进入电场前这一过程中,AB做匀速直线运动.已知MN两板间距大于细杆长度.试求:
(1)两板间电场强度的大小;
(2)上述匀速运动过程中速度大小;
(3)若AB以初动能Ek0从O处开始向下运动,恰好能使第10个小球过O点,求Ek0的大小.
如图所示,一质量为m=1 kg的小物块轻轻放在水平匀速运动的传送带上的A点,随传送带运动到B点,小物块从C点沿圆弧切线进入竖直光滑的半圆轨道恰能做圆周运动.已知圆弧半径R=0.9 m,轨道最低点为D,D点距水平面的高度h=0.8 m.小物块离开D点后恰好垂直碰击放在水平面上E点的固定倾斜挡板.已知物块与传送带间的动摩擦因数μ=0.3,传送带以5 m/s恒定速率顺时针转动(g取10 m/s2),试求:
(1)传送带AB两端的距离;
(2)小物块经过D点时对轨道的压力的大小;
(3)倾斜挡板与水平面间的夹角θ的正切值.