设椭圆
的左焦点为
, 离心率为
, 过点
且与
轴垂直的直线被椭圆截得的线段长为
.
(Ⅰ) 求椭圆的方程;
(Ⅱ) 设
分别为椭圆的左右顶点, 过点
且斜率为
的直线与椭圆交于
两点. 若
, 求
的值.
已知,命题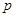 :
: ,命题
,命题 :
: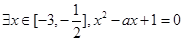 .
.
(1)若命题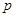 为真命题,求实数
为真命题,求实数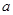 的取值范围;
的取值范围;
(2)若命题 为真命题,求实数
为真命题,求实数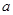 的取值范围;
的取值范围;
(3)若命题“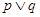 ”为真命题,且命题“
”为真命题,且命题“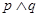 ”为假命题,求实数
”为假命题,求实数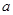 的取值范围.
的取值范围.
抽取某种型号的车床生产的10个零件,编号为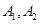 ,…,
,…,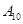 ,测量其直径(单位:cm),得到下面数据:
,测量其直径(单位:cm),得到下面数据:
| 编号 |
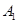 |
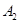 |
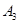 |
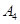 |
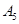 |
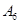 |
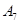 |
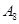 |
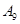 |
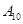 |
| 直径 |
1.51 |
1.49 |
1.49 |
1.51 |
1.49 |
1.48 |
1.47 |
1.53 |
1.52 |
1.47 |
其中直径在区间[1.49,1.51]内的零件为一等品.
(1)从上述10个零件中,随机抽取一个,求这个零件为一等品的概率;
(2)从一等品零件中,随机抽取2个.
①用零件的编号列出所有可能的抽取结果;
②求这2个零件直径相等的概率;
(3)若甲、乙分别从一等品中各取一个,求甲取到零件的直径大于乙取到零件的直径的概率.
用计算机随机产生的有序二元数组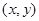 满足
满足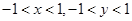 .
.
(1)求事件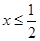 的概率;
的概率;
(2)求事件“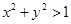 ”的概率.
”的概率.
已知数列 中,
中, ,下列伪代码的功能是求数列
,下列伪代码的功能是求数列 的第
的第 项
项 的值
的值 ,现给出此算法流程图的一部分.
,现给出此算法流程图的一部分.
(1)直接写出流程图中的空格①、②处应填上的内容,并写出 与
与 之间的关系;
之间的关系;
(2)若输入的 值为2015,求输出的
值为2015,求输出的 值(写明过程).
值(写明过程).
我县某中学为了配备高一新生中寄宿生的用品,招生前随机抽取部分准高一学生调查其上学路上所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图),其中上学路上所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].
(1)求直方图中 的值;
的值;
(2)如果上学路上所需时间不少于40分钟的学生应寄宿,且该校计划招生1800名,请估计新生中
应有多少名学生寄宿;
(3)若不安排寄宿的话,请估计所有学生上学的平均耗时(用组中值代替各组数据的平均值).