如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=4,DC=6,求AD的长. 
小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题.
请按照小萍的思路,探究并解答下列问题:
(1)分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D点的对称点为E、F,延长EB、FC相交于G点,证明四边形AEGF是正方形;
(2)设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值.
如图,已知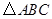 中,
中,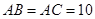 厘米,
厘米, 厘米,点
厘米,点 为
为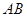 的中点.
的中点.
(1)如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后, 与
与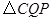 是否全等,请说明理由;
是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使 与
与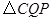 全等?
全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿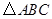 三边运动,求经过多长时间点P与点Q第一次在
三边运动,求经过多长时间点P与点Q第一次在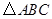 的哪条边上相遇?
的哪条边上相遇?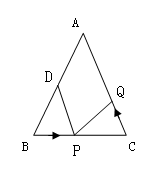
如图,△ABC的外部有一动点P(在直线BC上方),分别连结PB、PC,试确定∠BPC与∠BAC的大小关系。
在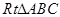 中,AC=5,BC=12,∠ACB=90°,P是AB边上的动点(与点A、B不重合),Q是BC边上的动点(与点B、C不重合),当PQ与AC不平行时,△CPQ可能为直角三角形吗?若有可能,请求出线段CQ的长的取值范围;若不可能,请说明理由。
中,AC=5,BC=12,∠ACB=90°,P是AB边上的动点(与点A、B不重合),Q是BC边上的动点(与点B、C不重合),当PQ与AC不平行时,△CPQ可能为直角三角形吗?若有可能,请求出线段CQ的长的取值范围;若不可能,请说明理由。
如图:已知,四边形ABCD中,AD//BC, DC⊥BC,已知AB=5,BC=6,cosB=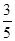 .
.
点O为BC边上的一个动点,连结OD,以O为圆心,BO为半径的⊙O分别交边AB于点P,交线段OD于点M,交射线BC于点N,连结MN.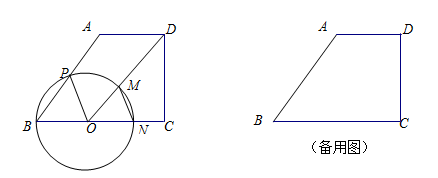
(1)当BO=AD时,求BP的长;
(2)点O运动的过程中,是否存在BP=MN的情况?若存在,请求出当BO为多长时BP=MN;若不存在,请说明理由;
(3)在点O运动的过程中,以点C为圆心,CN为半径作⊙C,请直接写出当⊙C存在时,⊙O与⊙C的位置关系,以及相应的⊙C半径CN的取值范围。
如图,在直角梯形ABCD中,AD∥BC,∠C=90°,BC=16,DC=12,AD=21。动点P从点D出发,沿射线DA的方向以每秒2两个单位长的速度运动,动点Q从点C出发,在线段CB上以每秒1个单位长的速度向点B运动,点P,Q分别从点D,C同时出发,当点Q运动到点B时,点P随之停止运动。设运动的时间为t(秒)。
(1)设△BPQ的面积为S,求S与t之间的函数关系式;
(2)当t为何值时,以B,P,Q三点为顶点的三角形是等腰三角形?
(3)是否存在时刻t,使得PQ⊥BD?若存在,求出t的值;若不存在,请说明理由。