规定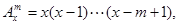 其中
其中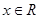 ,
,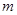 为正整数,且
为正整数,且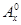 =1,这是排列数
=1,这是排列数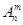 (
(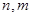 是正整数,
是正整数,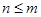 )的一种推广.
)的一种推广.
(Ⅰ) 求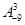 的值;
的值;
(Ⅱ)排列数的两个性质:①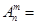
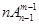 ,②
,②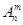
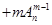
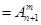 (其中m,n是正整数).是否都能推广到
(其中m,n是正整数).是否都能推广到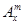 (
(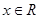 ,
,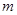 是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
是正整数)的情形?若能推广,写出推广的形式并给予证明;若不能,则说明理由;
(Ⅲ)已知函数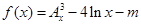 ,试讨论函数
,试讨论函数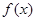 的零点个数.
的零点个数.
某工厂组织工人参加上岗测试,每位测试者最多有三次机会,一旦某次测试通过,便可上岗工作,不再参加以后的测试;否则就一直测试到第三次为止。设每位工人每次测试通过的概率依次为0.2,0.5,0.5。
(1)求工人甲在这次上岗测试中参加考试次数 的分布列;
的分布列;
(2)若有4位工人参加这次测试,求至少有一人不能上岗的概率。
在五棱锥P-ABCDE中,PA=AB=AE=2a,PB=PE= a,BC=DE=a,
a,BC=DE=a,
∠EAB=∠ABC=∠DEA=90°.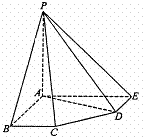 (1)求证:PA⊥平面ABCDE;
(1)求证:PA⊥平面ABCDE;
(2)若G为PE中点,求证: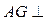 平面PDE
平面PDE
(3)求二面角A-PD-E的正弦值;
(4)求点C到平面PDE的距离
已知 ,q:x2-4x+4-9m2≤0 (m>0),若
,q:x2-4x+4-9m2≤0 (m>0),若 p是
p是 q的充分而不必要条件,求实数m的取值范围.
q的充分而不必要条件,求实数m的取值范围.
设函数 且
且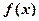 的图象在
的图象在 轴右侧的第一个最高点的横坐标为2。
轴右侧的第一个最高点的横坐标为2。
(1)求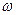 ;
;
(2)若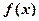 在区间[8,16]上的最大值为3,求m的值。
在区间[8,16]上的最大值为3,求m的值。
设三次函数h(x)=px3+qx2+rx+s满足下列条件:h(1)="1,h(-1)=" -1,在区间(-1,1)上分别取得极大值1和极小值-1,对应的极点分别为a,b。
(1)证明:a+b=0
(2)求h(x)的表达式
(3)已知三次函数f(x)=ax3+bx2+cx+d在(-1,1)上满足-1<f(x)<1。证明当|x|>1时,有|f(x)|<|h(x)|