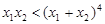已知函数f(x)=ax+x2,g(x)=xln a,a>1.
(1)求证:函数F(x)=f(x)-g(x)在(0,+∞)上单调递增;
(2)若函数y=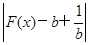 -3有四个零点,求b的取值范围;
-3有四个零点,求b的取值范围;
(3)若对于任意的x1,x2∈[-1,1]时,都有|F(x2)-F(x1)|≤e2-2恒成立,求a的取值范围.
(本小题满分12分)
如图所示,四棱锥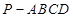 中,
中, 为正方形,
为正方形, ,
,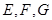 分别是线段
分别是线段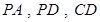 的中点. 求证:
的中点. 求证:
(1) //平面
//平面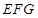 ;
;
(2)平面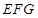 ⊥平面
⊥平面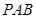 .
.
(本小题满分12分)
某产品按行业生产标准分成 个等级,等级系数
个等级,等级系数 依次为
依次为 ,其中
,其中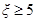 为标准
为标准 ,
, 为标准
为标准 ,产品的等级系数越大表明产品的质量越好. 已知某厂执行标准
,产品的等级系数越大表明产品的质量越好. 已知某厂执行标准 生产该产品,且该厂的产品都符合相应的执行标准.从该厂生产的产品中随机抽取
生产该产品,且该厂的产品都符合相应的执行标准.从该厂生产的产品中随机抽取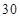 件,相应的等级系数组成一个样本,数据如下:
件,相应的等级系数组成一个样本,数据如下:
3 5 3 3 8 5 5 6 3 4
6 3 4 7 5 3 4 8 5 3
8 3 4 3 4 4 7 5 6 7
该行业规定产品的等级系数 的为一等品,等级系数
的为一等品,等级系数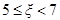 的为二等品,等级系数
的为二等品,等级系数 的为三等品.
的为三等品.
(1)试分别估计该厂生产的产品的一等品率、二等品率和三等品率;
(2)从样本的一等品中随机抽取2件,求所抽得2件产品等级系数都是8的概率.
(本小题满分12分)
已知数列 满足
满足 ,
,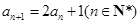 .
.
⑴求证:数列 是等比数列,并写出数列
是等比数列,并写出数列 的通项公式;
的通项公式;
⑵若数列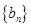 满足
满足 ,求
,求 的值.
的值.
(本小题满分12分)
已知函数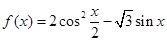 .
.
(1)求函数 的最小正周期和值域;
的最小正周期和值域;
(2)若 为第二象限角,且
为第二象限角,且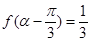 ,求
,求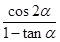 的值.
的值.
.(本小题满分15分)
已知函数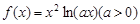
(Ⅰ)若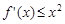 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围;
(Ⅱ)当 时,设函数
时,设函数 ,若
,若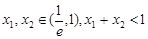 ,求证
,求证