某班将举行“庆祝建党90周年知识竞赛”活动,副市长安排小明购买奖品,下面两图是小明买回奖品时与班长的对话情境:
请根据上面的信息,解决问题:(1)试计算两种笔记本各买了多少本?(2)请你解释:小明为什么不可能找回68元?
两根同样长的蜡烛,点完一根粗蜡烛要2小时,而点完一根细蜡烛要1小时,一天晚上停电,小芳同时点燃了这两根蜡烛看书,若干分钟后来电了,小芳将两支蜡烛同时熄灭,发现粗蜡烛的长是细蜡烛2倍,问:停电﹙﹚分钟?
| A.30 | B.40 | C.50 | D.60 |
如图(1)在ΔABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.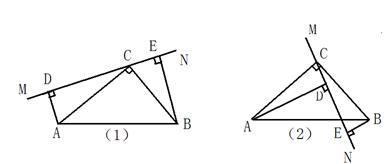
(1)求证:①ΔADC≌ΔCEB②DE=AD+BE
(2)当直线MN绕点C旋转到图(2)的位置时,DE、AD、BE 有怎样的关系?并加以证明.
如图,在ΔABC与ΔDCB 中,AC与BD 交于点E,且,∠A=∠D,AB=DC.
(1)求证:ΔABE≌ΔDCE
(2)当∠AEB=70°时,求∠EBC的度数.
如图,已知AE⊥BC,AD平分∠BAE,∠ADB=110°,∠CAE=20°.求∠B的度数.
如图:已知AB=AD,BC=DC,求证∠B=∠D.