已知命题 指数函数
指数函数 在
在 上单调递减,命题
上单调递减,命题 关于
关于 的方程
的方程
 的两个实根均大于3.若“
的两个实根均大于3.若“ 或
或 ”为真,“
”为真,“ 且
且 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
已知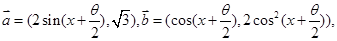 且
且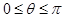 ,
,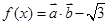 ,且
,且 为偶函数.
为偶函数.
(1)求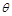 ;
;
(2)求满足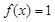 ,
, 的x的集合.
的x的集合.
设函数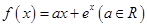
(1)若函数 有且只有两个零点
有且只有两个零点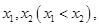 求实数
求实数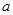 的取值范围;
的取值范围;
(2)当 时
时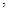 若曲线
若曲线 上存在横坐标成等差数列的三个点
上存在横坐标成等差数列的三个点
①证明: 为钝角三角形;
为钝角三角形;
②试判断 能否为等腰三角形
能否为等腰三角形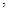 并说明理由
并说明理由
已知数列 共有
共有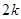 项
项 数列
数列 的前
的前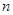 项的和为
项的和为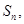 满足
满足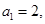
 其中常数
其中常数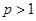
(1)求证:数列 是等比数列;
是等比数列;
(2)若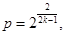 数列
数列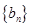 满足
满足 求数列
求数列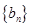 的通项公式
的通项公式
(3)对于(2)中的数列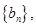 记
记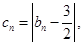 求数列
求数列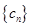 的前
的前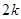 项的和
项的和
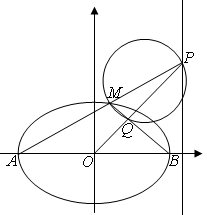
如图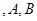 是椭圆
是椭圆 的左右顶点
的左右顶点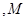 是椭圆上异于
是椭圆上异于 的任意一点
的任意一点 直线
直线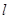 是椭圆的右准线
是椭圆的右准线
(1)若椭圆 的离心率为
的离心率为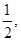 直线
直线 求椭圆
求椭圆 的方程;
的方程;
(2)设直线 交
交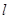 于点
于点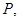 以
以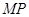 为直径的圆交
为直径的圆交 于
于 若直线
若直线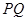 恰好过原点
恰好过原点 求椭圆
求椭圆 的离心率
的离心率