某校七年级学生到野外活动,为测量一池塘两端A,B的距离,甲、乙、丙三位同学分别设计出如下几种方案:
甲:如图①,先在平地取一个可直接到达A,B的点C,再连接AC,BC,并分别延长AC至D,BC至E,使DC=AC,EC=BC,最后测出DE的长即为A,B的距离。
乙:如图②,先过点B作AB的垂线BF,再在BF上取C,D两点,使BC=CD,接着过点D作BD的垂线DE,交AC的延长线于点E,则测出DE的长即为A,B的距离。
丙:如图③,过点B作BD⊥AB,再由点D观测,在AB的延长线上取一点C,使∠BDC=∠BDA,这时只要测出BC的长即为A,B的距离。
(1)以上三位同学所设计的方案,可行的有_______________;
(2)请你选择一可行的方案,说说它可行的理由。
在一个黑色的布口袋里装着白、红两种颜色的小球,它们除了颜色之外没有其它区别,其中白球2个、红球1个,球在袋中进行搅匀.
(1)若随机地从袋中摸出1个球,则摸出红球的概率是多少?
(2)随机地从袋中摸出1个球,放回搅匀再摸出第二个球.请你用画树状图或列表的方法表示所有等可能的结果,并求两次都摸出白球的概率.
如图,已知AB=AC,AD=AE,∠1=∠2.求证:BD=CE.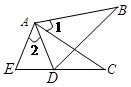
先化简,再求值: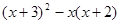 ,其中
,其中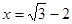 .
.
二次函数y=-x2+4x的顶点M,与x轴交于O点和A点.直线y=-2x向上平移 m个单位交直线OM于点E,交x轴于点C,交y轴于点D.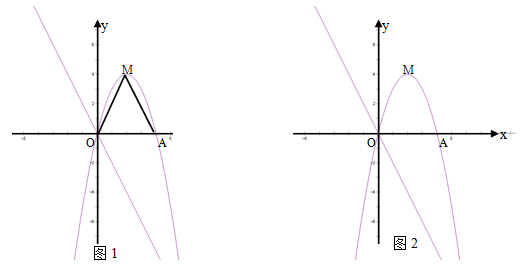
(1)当△EOC的面积等于△AOM面积的一半,求m的值.
(2)已知点P是二次函数y=-x2+4x图象在y轴右侧部分上的一个动点,若∠PCD=900且△PCD与△OCD
相似,求P点坐标.
如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
可证:AE⊥BF;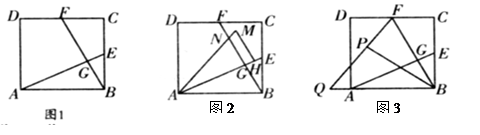
(1)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM,如图2,若AM和BF相交
于点N,当正方形ABCD的面积为4时,求四边形GHMN的面积.
(2)将△BCF沿BF对折,得到△BPF,如图3,延长FP交BA的延长线于点Q,求sin∠BQP的值;