乘法公式的探究及应用:
探究问题:
如图1是一张长方形纸条,将其剪成长短两条后刚好能拼成图2,如图所示。
(1)则图1长方形纸条的面积可表示为________________(写成多项式乘法的形式)。
(2)拼成的图2中阴影部分面积可表示为________________(写成两数平方差的形式)。
(3)比较两图的阴影部分面积,可以得到乘法公式____________。
结论运用:
(4)应用所得的公式计算: =____________________。
=____________________。 =___________________。
=___________________。
拓展运用:
(5)计算: 。
。
(本大题共6分)如图所示,在△ABC中,∠BAC=90°,AD⊥BC于D,∠ACB的平分线交AD于E,交AB于F,FG⊥BC于G,请猜测AE与FG之间有怎样的数量关系,并说明理由.
(本大题共6分)等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.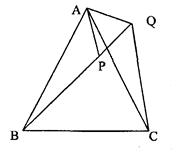
(本大题共6分)墙上钉了一根木条,小明想检验这根木条是否水平,他拿来一个测平仪,在这个测平仪中,AB=AC,BC边的中点D处挂了一个重锤,小明将BC边与木条重合,观察此时重锤是否过A点。如果过A点,那么这根木条就是水平的,你能说明其中的道理吗?
(本大题共6分)如图,已知△ABC.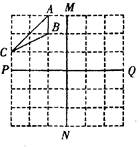
(1)画出△A1B1C1,使△A1B1C1和△ABC关于直线MN成轴对称.
(2)画出△A2B2C2,使△A2B2C2和△ABC关于直线PQ成轴对称.
(3)△A1B1C1与△A2B2C2成轴对称吗?若成,请在图上画出对称轴;若不成,说明理由.
(本大题共6分)若m是169的正的平方根,n是121的负的平方根,求:
(1)m+n的值;
(2)(m+n)2的平方根.