(本大题共6分)若m是169的正的平方根,n是121的负的平方根,求:
(1)m+n的值;
(2)(m+n)2的平方根.
学习了统计知识后,班主任王老师叫班长就本班同学的上学方式进行了一次调查统计,图1和图2是他通过收集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题:
(1)在扇形统计图中,计算出“步行”部分所对应的圆心角的度数;
(2)求该班共有多少名学生;
(3)在图1中,将表示“乘车”的部分补充完整.
A,B两地相距18公里,甲工程队要在A,B两地间铺设一条输送天然气管道,乙工程队要在A,B两地间铺设一条输油管道.已知甲工程队每周比乙工程队少铺设1公里,甲工程队提前3周开工,结果两队同时完成任务,求甲、乙两工程队每周各铺设多少公里管道?
如图,甲、乙两栋高楼的水平距离BD为90米,从甲楼顶部C点测得乙楼顶部A点的仰角α为30°,测得乙楼底部B点的俯角β为60°,求甲、乙两栋高楼各有多高?(计算过程和结果都不取近似值)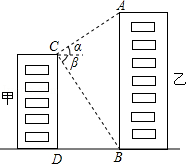
如图,在平行四边形ABCD中,点E是边AD的中点,BE的延长线与CD的延长线相交于点F.
(1)求证:△ABE≌△DFE;
(2)试连接BD、AF,判断四边形ABDF的形状,并证明你的结论.
先化简,再求值: ,其中
,其中 .
.