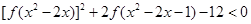在平面直角坐标系中,以坐标原点为极点,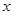 轴的非负半轴为极轴建立坐标系.已知点
轴的非负半轴为极轴建立坐标系.已知点 的极坐标为
的极坐标为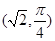 ,直线的极坐标方程为
,直线的极坐标方程为 ,且点
,且点 在直线上.
在直线上.
(1)求 的值及直线的直角坐标方程;
的值及直线的直角坐标方程;
(2)圆c的参数方程为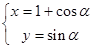 ,(
,(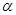 为参数),试判断直线与圆的位置关系.
为参数),试判断直线与圆的位置关系.
已知直三棱柱 中,△
中,△ 为等腰直角三角形,∠
为等腰直角三角形,∠ =90°,且
=90°,且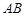 =
= ,
, 、
、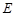 、
、 分别为
分别为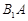 、
、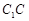 、
、 的中点.
的中点.
(1)求证: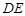 ∥平面
∥平面 ;
;
(2)求证: ⊥平面
⊥平面 ;
;
(3)求二面角 的余弦值
的余弦值
某校为了探索一种新的教学模式,进行了一项课题实验,甲班为实验班,乙班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,测试成绩的分组区间为 80,90
80,90 、
、 90,100
90,100 、
、 100,110
100,110 、
、 110,120
110,120 、
、 120,130
120,130 ,由此得到两个班测试成绩的频率分布直方图:
,由此得到两个班测试成绩的频率分布直方图: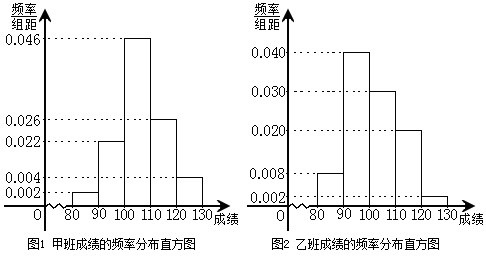
(I)完成下面2×2列联表,你能有97.5 的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
| 成绩小于100分 |
成绩不小于100分 |
合计 |
|
| 甲班 |
 |
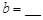 |
50 |
| 乙班 |
 |
 |
50 |
| 合计 |
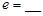 |
 |
100 |
(II)现从乙班50人中任意抽取3人,记 表示抽到测试成绩在[100,120
表示抽到测试成绩在[100,120 的人数,求
的人数,求 的分布列和数学期望
的分布列和数学期望 .
.
附: ,其中
,其中
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
 |
2.072 |
2.706 |
3.841 |
5.204 |
6.635 |
7.879 |
10.828 |
已知函数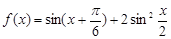 .
.
(1)求函数 的单调递增区间;
的单调递增区间;
(2)记△ 的内角
的内角 、
、 、
、 所对的边长分别为
所对的边长分别为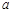 、
、 、
、 ,若
,若 ,△
,△ 的面积
的面积 ,
, ,求
,求 的值.
的值.
已知点(1,2)是函数 的图象上一点,数列
的图象上一点,数列 的前
的前 项和是
项和是 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,求数列
,求数列 的前
的前 项和
项和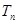
)已知函数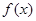 满足对一切
满足对一切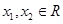 都有
都有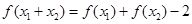 ,且
,且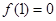 ,当
,当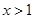 时有
时有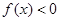 .
.
(1)求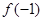 的值;
的值;
(2)判断并证明函数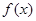 在
在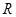 上的单调性;
上的单调性;
(3)解不等式: