用下图所示的转盘进行配紫色(红色与蓝色配成)游戏:其中A转盘蓝色部分占整个转盘的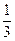 .求游戏者获胜的概率?
.求游戏者获胜的概率?
袋中有1个白球,2个黄球,问
(1)从中一次性地随机摸出2个球,都是黄球的概率是多少?
(2)先从中摸出一球,再从剩下的球中摸出一球,两次都是黄球的概率是多少?
(3)先从中摸出一球,将它放回口袋中后,再摸一次,两次都是黄球的概率是多少?
质地均匀的三个几何体A、B、C. A是硬币,正面涂红色,反面涂黄色;B是正四面体涂了红黄蓝白四色,每面一色;C是正方体,每面涂一色,涂有红黄蓝三色,每种颜色两个面,在水平地面上依次投A、B、C各一次,几何体与地面接触的面的颜色称为“保留色”。
(1)求A、B、C的“保留色”相同的概率;
(2)求A、B、C的“保留色”恰为两个红色的概率;
(3)求A、B、C的“保留色”互不相同的概率;
从原点出发的某质点M,按向量a=(0,1)移动的概率为 ,按向量b=(0,2)移动的概率为
,按向量b=(0,2)移动的概率为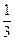 ,设M可到达点(0,n)的概率为Pn
,设M可到达点(0,n)的概率为Pn
(1)求P1和P2的值;(2)求证: =
=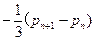 ;(3)求
;(3)求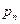 的表达式。
的表达式。
多项飞碟是奥运会的竞赛项目,它是由抛靶机把碟靶(射击的目标)在一定范围内从不同的方向飞出,每抛出一个碟靶,就允许运动员射击两次.一运动员在进行训练时,每一次射击命中碟靶的概率P与运动员离碟靶的距离S(米)成反比,现有一碟靶抛出后S(米)与飞行时间t(秒)满足S=15(t+1),(0≤t≤4).假设运动员在碟靶飞出后0.5秒进行第一次射击,且命中的概率为0.8,如果他发现没有命中,则通过迅速调整,在第一次射击后经过0.5秒进行第二次射击,求他命中此碟靶的概率?