如图,在正方体 中.
中.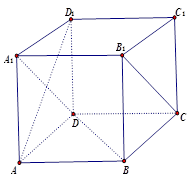
(1)求证: 平面
平面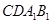 ;
;
(2)求直线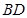 与平面
与平面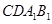 所成的角.
所成的角.
(本小题共13分)为了解某地区中学生的身体发育状况,拟采用分层抽样的方法从甲、乙、丙三所中学抽取6个教学班进行调查.已知甲、乙、丙三所中学分别有12,6,18个教学班.
(Ⅰ)求从甲、乙、丙三所中学中分别抽取的教学班的个数;
(Ⅱ)若从抽取的6个教学班中随机抽取2个进行调查结果的对比,求这2个教学班中至少有1个来自甲学校的概率.
(本小题共14分)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC,M,N分别是CC1,AB的中点.
(Ⅰ)求证:CN⊥AB1;
(Ⅱ)求证:CN //平面AB1M.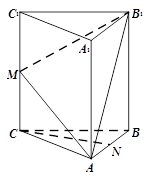
(本小题共13分)已知函数 .
.
(Ⅰ)求函数 的最小正周期和值域;
的最小正周期和值域;
(Ⅱ)若 为第二象限角,且
为第二象限角,且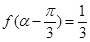 ,求
,求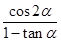 的值.
的值.
(本小题共13分)若有穷数列{an}满足:(1)首项a1=1,末项am=k,(2)an+1= an+1或an+1="2an" ,(n=1,2,…,m-1),则称数列{an}为k的m阶数列.
(Ⅰ)请写出一个10的6阶数列;
(Ⅱ)设数列{bn}是各项为自然数的递增数列,若 ,且
,且 ,求m的最小值.
,求m的最小值.
(考生务必将答案答在答题卡上,在试卷上作答无效)
(本小题共14分)设函数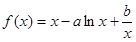 在
在 处取得极值.
处取得极值.
(Ⅰ)求 与
与 满足的关系式;
满足的关系式;
(Ⅱ)若 ,求函数
,求函数 的单调区间;
的单调区间;
(Ⅲ)若 ,函数
,函数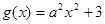 ,若存在
,若存在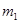 ,
,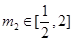 ,使得
,使得 成立,求
成立,求 的取值范围.
的取值范围.